Haremos primero una distinción entre los dos tipos diferentes posibles de curvatura que puede haber sobre una superficie: la curvatura intrínseca y la curvatura extrínseca. Consideremos primero la superficie de un cilindro, la cual como vimos previamente se obtiene enrollando una hoja plana de papel. Uno puede pensar que la superficie de un cilindro es curva puesto que dicha superficie está “redonda” en cierta dirección en torno al eje de simetría. Esta es una curvatura extrínseca, ya que no tiene relación alguna con el espacio tri-dimensional plano (en la hoja del cilindro) del cual forma parte. Uno puede formar la superficie de un cilindro con el simple hecho de enrollar un pedazo plano de papel sin necesidad de tener que cortar o arrugar el papel en lo más mínimo, de modo tal que la geometría intrínseca es la misma es la misma que la del pedazo de papel original, es una geometría plana, lo cual significa que la distancia original entre dos puntos cualesquiera sobre la superficie del papel sigue siendo la misma antes y después del enrollamiento. Las líneas paralelas trazadas sobre la hoja plana de papel original siguien siendo paralelas después de haber sido enrollado el papel para formar un cilindro, lo cual implica que al permanecer invariable la validez del quinto postulado de la geometría Euclideana (por un punto exterior a una recta dada sólo es posible trazar una línea paralela a la recta dada) la superficie del cilindro sigue siendo una geometría Euclideana, todos los resultados y teoremas clásicos de la geometría Euclideana plana siguen siendo válidos sobre la superficie de un cilindro (la suma de los ángulos internos de un triángulo cualquiera es igual a 180 grados, el cuadrado de la hipotenusa de un triángulo rectántulo es igual a la suma de los cuadrados de los catetos, etc.) Para una hormiga confinada a vivir sobre la superficie de un cilindro, la superficie del cilindro sería una superficie plana en todos sentidos, no tendría forma alguna de detectar la curvatura haciendo mediciones extremadamente precisas de ángulos sobre dicha superficie. Lo único curioso que encontraría es que viajando hacia adelante siempre en línea recta, después de una cantidad finita de tiempo descubriría asombrada haber regresado al mismo punto en el cual empezó su travesía. La geometría intrínseca de una hoja n-dimensional considera únicamente la relación que pueda haber entre los puntos de las trayectorias confinados a su superficie, mientras que la geometría extrínseca proviene del considerar a dicha superficie como parte de un espacio formado por un mayor número de dimensiones como lo es el caso de la superficie del cilindro. De este modo, la geometría extrínseca descansa sobre la suposición de la existencia de espacios multidimensionales con un mayor número de dimensiones.
En la Relatividad General, cuando hablamos de la curvatura del espacio-tiempo, estamos hablando de una curvatura intrínseca, puesto que todas las líneas del mundo están confinadas a permanecer en un espacio cuatri-dimensional; en la Relatividad General en su formulación original no hay espacios de cinco dimensiones o más. Desde la perspectiva de la Relatividad General, si habitamos en un mundo que forma parte de algo que ocupe más de cuatro dimensiones, ello no es cosa que nos concierna, puesto que de cualquier manera no podemos salir fuera hacia esa “quinta dimensión”; lo único en lo que estamos interesados es en la geometría intrínseca del espacio-tiempo.
La superficie del cilindro es intrínsecamente plana. Pero si empezamos a considerar la superficie de una esfera, entonces las cosas cambian dramáticamente. Para darnos cuenta de ello, considérese la siguiente figura en la cual tenemos un triángulo esférico formado por el área delimitada por tres círculos máximos (que son las geodésicas o “líneas rectas” sobre la superficie de una esfera):
Sobre la superficie de una esfera como ésta, la geometría deja de ser Euclideana. En ella, dos líneas inicialmente paralelas dejan de ser paralelas desde el momento en que son trazadas. Si trazamos sobre la geodésica AB dos líneas muy cercanas entre sí que sean perpendiculares a dicha geodésica, eventualmente terminarán cruzándose. Por otro lado, la suma de los ángulos internos α, β y γ del triángulo ABC ya no es igual a 180 grados, y de hecho siempre será mayor que 180 grados. Podemos trazar sin dificultad alguna sobre la superficie de una esfera un triángulo cuyos ángulos internos sean todos ángulos rectos, y cuya suma será igual a 270 grados:
Otra diferencia que podemos encontrar la tenemos si trazamos sobre una hoja plana un “triángulo” hecho con curvas, el cual podemos tomar como la proyección de un triángulo esférico sobre una imagen tomada por una cámara fotográfica, y empezando en un punto de dicho triángulo empezamos a trazar líneas horizontales que para nosotros serán líneas perfectamente paralelas:
Si empezamos desde el punto A trazando una línea recta con forma de flecha (de color rojo) representando un vector, y nos vamos desplazando en sentido contrario a las manecillas del reloj hasta llegar al punto B y después al punto C para finalmente regresar al punto A, trazando más líneas horizontales al ir haciendo el recorrido, al regresar al punto A el vector final será paralelo al vector inicial, ambos apuntarán en la misma dirección. Pero si llevamos a cabo un procedimiento similar sobre la superficie de una esfera, entonces tenemos algo interesante:
En este caso, supóngase que empezamos trazando flechas perfectamente paralelas a lo largo de la geodésica que va desde el punto A hasta el punto N (el cual podemos tomar como el polo Norte). Estas flechas o vectores serán desde luego las tangentes a la geodésica que va desde el punto A hasta el punto N. De la misma manera, una vez que hemos llegado al punto N, trazamos una paralela a la última tangente que construída al llegar a N pero moviéndonos a lo largo de la geodésica que va desde el punto N hasta el punto B, lo cual significa que la paralela trazada será una perpendicular al arco NB, y tras esto vamos trazando otras perpendiculares iguales a lo largo del arco NB, todas las cuales serán paralelas entre sí, hasta llegar al punto B. Hasta aquí, todo parece en orden.
Ahora supóngase que continuamos el procedimiento después de haber llegado desde el punto N hasta el punto B trazando rectas paralelas, y empezamos a trazar más paralelas yéndonos del punto B hasta el punto A. Recuérdese que todas estas rectas las estamos trazando mediante escuadra y compás tan paralelas como no es posible.
Es al completar el circuito llegando al punto A cuando nos topamos con una sorpresa. La línea “paralela” en el punto A al llegar a dicho punto desde el punto B no apunta en la misma dirección que la de la línea “paralela” inicial. De hecho, el campo vectorial ha experimentado una rotación de α grados en nuestra construcción sobre la superficie esférica. De este modo, si partimos desde un punto cualquiera del globo terráqueo siguiendo una ruta geodésica y vamos trazando tangentes sobre dicha ruta, todas las cuales serán paralelas entre sí al irlas trazando, y continuamos trazando más paralelas conforme hacemos el recorrido que correspondería a una trayectoria sobre las líneas de un triángulo esférico, entonces al completar un circuito cerrado encontramos que las líneas han dejado de ser paralelas. Es el circuito cerrado el que ha dado origen a la discrepancia.
La construcción que acabamos de llevar a cabo es conocida como el transporte paralelo, porque vamos “transportando” una paralela de un punto a otro trazándolas tan paralelas la una a la otra como nos sea posible. Pero por lo que acabamos de ver, no nos es posible intentar definir -sobre una hoja de trazado curva- campos vectoriales globalmente paralelos. Aún nos es posible definir un paralelismo local, especificando cómo mover un vector de un punto a otro sobre una hoja de trazado curva de modo tal que el vector trasladado mantenga la misma dirección y la misma longitud, pero el resultado de tal transporte paralelo dependerá del tipo de curvatura y sobre todo de la ruta seguida, por lo que no se puede afirmar de modo general que un vector trazado en un punto A sea paralelo a otro vector B sobre una superficie curva.
En la siguiente figura tenemos un vector V (de color rojo) que ha sido objeto de un transporte paralelo a lo largo de una curva en la cual una tangente cualquiera de dicha curva es un vector U (de color azul) que viene siendo igual a U = dx/dλ en donde dλ es un parámetro que puede ser un segmento infinitesimal de arco o un intervalo infinitesimal de tiempo:
Existe un método de aproximación de primer orden con cierta justificación matemática sobre el paralelogramoide de Levi-Civita para ir construyendo (transportando) un vector V a lo largo de una ruta geodésica, conocido como la escalera de Schild, ilustrado en el siguiente diagrama:
El método de construcción es el siguiente:
(1) Empezamos con un segmento de geodésica como el que muestra la figura de arriba, sobre el cual está puesto el vector V = A0X0 que es el vector que será movido a lo largo de la geodésica mediante el transporte paralelo.
(2) Seleccionamos otro punto A1 sobre la geodésica que esté cercano al punto A0, en la dirección hacia la cual será movido el vector original.
(3) Trazamos una recta que conecte la punta del vector A0X0 con el punto A1, y hecho esto marcamos el punto medio de dicha recta, que aquí llamaremos P1.
(4) Constrúyase la geodésica A0P1 y extiéndase la misma hasta el punto X1, de modo tal que la longitud paramétrica de A0X1 sea el doble de la longitud A0P1.
(5) Finalmente, constrúyase la geodésica A1X1, con lo cual el vector original ha sido desplazado en transporte paralelo hacia una nueva posición.
La figura muestra dos peldaños de la escalera.
Para poder continuar adelante, daremos ahora un repaso a la estructura matemática que está detrás de los conceptos de la tangente a una curva espacial en un punto cualquiera de dicha curva.
Intuitivamente, el concepto de la recta tangente a una curva espacial no ofrece mucha dificultad. En la siguiente figura:
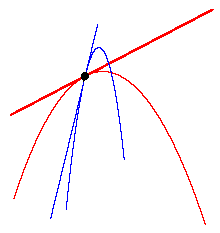
en donde sobre la superficie del paraboloide se ha trazado una curva espacial (de color rojo, la cual no necesariamente es la geodésica sobre dicha superficie) se ha trazado una recta tangente a dicha curva espacial (de color verde). Y en la siguiente figura, tenemos dos parábolas planas, una de color rojo y la otra de color azul, cada una de las cuales tiene trazada su propia recta tangente en un punto común a ambas (del mismo color que hace corresponder a la curva espacial con la tangente que le toca):
Como puede verse en ambas figuras, la tangente puesta en cierto punto P de una curva espacial apunta en la misma dirección hacia la cual se está moviendo en el espacio dicho punto. A cada punto de una misma curva espacial corresponderá una tangente diferente.
Podemos definir formalmente a la tangente de una curva en un punto P de dicha curva como el proceso límite de varias secantes trazadas a través de dicho punto en donde la distancia h entre los dos puntos P y Q de una secante sobre la curva se va disminuyendo arbitrariamente hasta que h toma un valor infinitesimalmente pequeño:
En un sistema tri-dimensional de coordenadas Cartesianas, si tenemos una curva espacial cuyas componentes en cada uno de los tres ejes están especificadas con funciones independientes de un parámetro como t (en función del tiempo) o como s (en función del arco de longitud de la curva):
x = x(t)___y = y(t)___z = z(t)
entonces si agrupamos estas componentes en un triplete ordenado al cual podemos designar como U:
U = [x(t), y(t), z(t)]
el vector tangente dU/dt (o dU/ds, en su caso) estará dado simplemente por la derivada respectiva de cada componente:
Para simbolizar lo mismo, se acostumbra usar también la notación de los vectores unitarios de base, los cuales son de longitud 1 y que en coordenadas Cartesianas son i, j y k, con lo cual:
Otra notación alterna con vectores unitarios de base utilizada frecuentemente en muchos textos es la siguiente:
Todas estas notaciones sirven para indicar exactamente lo mismo, un triplete ordenado de elementos que deben mantenerse separados para efectos de cálculo matemático.
Para distinguir a un vector tangente dU/dt de longitud arbitraria obtenido sobre un punto P de una curva espacial de un vector tangente unitario cuya longitud es siempre igual a la unidad, tenemos que dividirlo entre la expresión que nos dé la magnitud ║dU/dt║ de dicho vector. Podemos denotar a este último como T:
T = (dU/dt) /║dU/dt║
PROBLEMA (5): Suponiendo que una curva C está definida por las ecuaciones paramétricas x = x(s), y = y(s), z = z(s), en donde s es una longitud de arco de la curva C medida desde un punto fijo en C, demostrar que si r es un vector posición de cualquier punto en la curva C entonces dr/ds es un vector tangente unitario a la curva C en dicho punto.
Si r es el vector posición que nos dá las coordenadas de la punta de un vector flecha a partir del origen (0,0,0), entonces:
r = (x, y, z)
Podemos representar el triplete de componentes en vectores unitarios de base i, j y k para simplificar el desarrollo de la solución:
r = x i + y j + z k
Tomando la derivada con respecto a un elemento infinitesimal de longitud, el vector:
es una tangente a la curva recorrida por la punta del vector posición en base al procedimiento de construcción dado arriba. La magnitud de este vector está dada por:
Usando la relación Pitagórica para un elemento infinitesimal de longitud:
ds² = dx² + dy² + dz²
Reagrupando y usando la relación tenemos entonces que:
║dr/ds║ = √(dx² + dy² + dz²)/(ds)²
║dr/ds║ = √(dx² + dy² + dz²)/(dx² + dy² + dz²)²
║dr/ds║ = 1
║dr/ds║ = √(dx² + dy² + dz²)/(dx² + dy² + dz²)²
║dr/ds║ = 1
Entonces el vector tangente ║dr/ds║ = 1 es un vector unitario.
PROBLEMA: (1) Encontrar un vector unitario tangente a cualquier punto sobre la curva espacial cuyas ecuaciones paramétricas son las siguientes:
x = t² + 1
y = 4t - 3
z = 2t² - 6t
y = 4t - 3
z = 2t² - 6t
y (2) encontrar la tangente unitaria en el punto en donde t = 2.
(1) Para encontrar un vector tangente a cualquier punto sobre la curva, obtenemos primero:
dx/dt = 2t
dy/dt = 4
dz/dt = 4t - 6
dy/dt = 4
dz/dt = 4t - 6
En notación de triplete, el vector tangente a cada punto de la curva está dado por:
dr/dt = (2t, 4, 4t - 6)
Y en notación con vectores unitarios de base, podemos escribir la misma respuesta ya sea como:
dr/dt = (2t) i + 4 j - (4t - 6) k
o como:
dr/dt = (2t) e1 + 4 e2 - (4t - 6) e3
Ambas notaciones sirven para indicar exactamente lo mismo, un triplete ordenado de elementos que deben mantenerse separados para efectos de cálculo matemático.
La longitud de este vector tangente dr/dt es algo que puede variar de un punto a otro sobre la curva espacial. Para que el vector tangente sea unitario en cualquier punto de la curva, tenemos que dividirlo entre la magnitud de dicho vector, la cual es:
║dr/dt║ = √(dx/dt)² + (dy/dt)² + (dz/dt)²
║dr/dt║ = √(2t)² + (4)² + (4t - 6)²
║dr/dt║ = √(2t)² + (4)² + (4t - 6)²
Usando notación de vectores unitarios de base, el vector tangente unitario T sobre cualquier punto de la curva será:
T = (dr/dt) /(║dr/dt║)
(2) En el punto t = 2, el vector tangente unitario será;
Haremos ahora un repaso de otro concepto que utilizaremos en nuestra discusión posterior, el concepto de la derivada direccional. Para ello, definiremos primero el operador diferencial del o nabla en tres dimensiones en coordenadas rectangulares (Cartesianas) de la siguiente manera:
Siendo este operador un operador vectorial, aplicarlo sobre una función escalar φ cualesquiera nos producirá un campo vectorial, el campo vectorial ∇φ, al cual se le dá el nombre de gradiente.
Recurriendo a coordenadas generalizadas xk, podemos extender también la definición del operador vectorial ∇ de tres dimensiones a un espacio 4-dimensional:
PROBLEMA: Encontrar el gradiente de las siguientes funciones escalares:
(1) φ = x² + y² + z²
(2) φ = 5 + 2x -4xy² + 3z
(3) φ = xyz
(4) φ = x² - y² - z²
Usando notación de vectores unitarios de base:
(1) ∇φ = 2x i + 2y j + 2z k
(2) ∇φ = (2 - 4y²) i - 8xy j + 3 k
(3) ∇φ = yz i + xz j + yz k
(4) ∇φ = 2x i - 2y j - 2z k
La componente del vector gradiente ∇φ que apunta en la dirección de un vector unitario V se obtiene con el producto escalar de ambos, o sea ∇φ·V, y se define formalmente como la derivada direccional de la función escalar φ a lo largo de la dirección del vector V. Geométricamente hablando, en cierta forma es igual a la magnitud de la proyección del vector ∇φ en la dirección hacia la cual apunta el vector V. Físicamente, esto se interpreta como la razón de cambio de φ en la dirección de V en cierto punto preseleccionado del espacio a lo largo de una trayectoria.
PROBLEMA: Encontrar la derivada direccional del siguiente campo escalar:
φ = x²yz + 4xz²
en el punto (1, -2, -1) en la dirección del vector:
v = (2, -1, -2)
El primer paso en la solución de este problema consiste en la determinación del campo vectorial ∇φ a partir del campo escalar φ mediante la aplicación del operador vectorial ∇ a φ. Lo haremos aquí usando notación de vectores unitarios de base en lugar del triplete ordenado de números con el objeto de simplificar la lectura de los pasos:
∇φ = ∇(x²yz + 4xz²)
∇φ = (2xyz + 4z²) i + x²z j + (x²y + 8xz) k
∇φ = (2xyz + 4z²) i + x²z j + (x²y + 8xz) k
En el punto (1, -2, -1), el vector que pertenece al campo vectorial ∇φ tiene el siguiente valor:
∇φ = (4 + 4) i + (-1) j + (-2 - 8) k
∇φ = 8i - j - 10k
∇φ = 8i - j - 10k
Antes de encontrar la derivada direccional en el punto (1, -2, -1) en la dirección del vector v = (2, -1, -2), normalizaremos dicho vector para que tenga una longitud igual a la unidad:
V = v / ║v║
V = (2 i - j - 2k) /√(2)² + (-1)² + (-2)²
V = (2 i - j - 2k) /3
V = (2/3) i - (1/3) j - (2/3) k
V = (2 i - j - 2k) /√(2)² + (-1)² + (-2)²
V = (2 i - j - 2k) /3
V = (2/3) i - (1/3) j - (2/3) k
La derivada direccional que estamos buscando la obtenemos tomando el producto escalar de los vectores ∇φ y V:
∇φ · V = [8i - j - 10k ] · [(2/3) i - (1/3) j - (2/3)] k
∇φ · V = (8) (2/3) + (-1) (-1/3) + (-10)(-2/3)
∇φ · V = 37/3
∇φ · V = (8) (2/3) + (-1) (-1/3) + (-10)(-2/3)
∇φ · V = 37/3
En virtud de que la derivada direccional es positiva, esto nos dice que φ está aumentando en esta dirección.
Si hemos de definir lo que hemos visto arriba en términos un poco más elegantes y más formales, usando coordenadas generalizadas, podemos decir que si tenemos una función escalar φ que dependa de varias coordenadas x1, x2, x3, ..., etc.:
a lo largo de un vector v (tangente a una curva espacial):
entonces la derivada direccional de esa función escalar φ a lo largo del vector v está definida mediante el límite:
Esta definición intenta resumir todo lo que ya se ha señalado arriba, y en realidad no es más que la representación formal del producto escalar:
∇φ(x) · v
que frecuentemente se resume simplemente como:
Habiendo visto ya lo que es la derivada direccional, estamos preparados para ver lo que es la derivada absoluta de un tensor, la cual se representa con la siguiente simbología en el caso de un tensor covariante A:
Esta simbología así como el uso de la palabra “derivada absoluta” son desafortunados porque pudieran dar la falsa impresión de que la derivada absoluta de un tensor equivale simplemente a la diferenciación de un tensor, lo cual no es así, porque la derivada absoluta es la extensión al cálculo tensorial del concepto de la derivada direccional, y como lo vimos arriba, la derivada direccional no es simplemente la diferenciación de un vector, sino que es algo sobre lo cual se aplica posteriormente un producto vectorial escalar con una tangente para obtener la proyección
Aclarado lo anterior, definimos a la derivada absoluta de un tensor o derivada intrínseca de un tensor de la siguiente manera en caso de que se trate de un tensor contravariante Tj:
Compárese esta definición con la definición de la derivada direccional. Al igual que en el caso de la derivada direccional en donde tenemos que obtener primero el vector gradiente ∇φ mediante la aplicación del operador diferencial vectorial ∇, también para obtener la derivada absoluta tenemos que obtener la derivada covariante del tensor T, lo cual es simbolizado como Tj,q mediante la notación de la coma puesta en el sub-índice del tensor antes de la letra q que representa a la coordenada general con respecto a la cual se toma la derivada covariante. Al igual que en el caso de la derivada direccional en donde vamos a efectuar a cabo el producto escalar del vector gradiente ∇φ con el vector V que es la tangente a la curva espacial sobre la cual se lleva a cabo la operación, en la derivada absoluta también efectuamos una operación de producto escalar con cada uno de los componentes dxq/dt que agrupados bajo un vector vienen siendo también una tangente a una curva espacial. Y al igual que en el caso de la derivada direccional en donde llevamos a cabo un producto escalar entre los vectores ∇φ y V, en el caso de la derivada absoluta igualmente llevamos a cabo un producto interno entre los tensores Tj,q y dxq/dt mediante una operación de contracción como lo requiere la convención de sumación para índices repetidos, lo cual a fin de cuentas viene siendo lo mismo que la toma del producto escalar entre ambos tensores. Obsérvese el uso de la palabra intrínseca en el otro nombre que se le puede dar a la derivada absoluta de un tensor. Esto tiene una connotación geométrica directa con el concepto de la curvatura intrínseca dado arriba al inicio de esta entrada. Es precisamente de lo que se trata. Obsérvese también que el resultado final de las operaciones combinadas en el caso de la derivada absoluta viene siendo un tensor del mismo tipo y del mismo orden que el tensor original. Esto quiere decir que si obtenemos la derivada absoluta de un tensor contravariante de orden uno, el resultado será también un tensor contravariante de orden uno.
PROBLEMA: Partiendo del tensor contravariante Ai, y formando el producto interno de la derivada covariante Ai, j con el vector tangente dxi/dt a una curva espacial, demostrar la siguiente relación:
Todas las operaciones y demostraciones a ser llevadas a cabo en problemas de este tipo tienen su punto de partida en una definición tensorial como la siguiente:
El primer paso consiste en tomar la derivada covariante del tensor Ai:
Tomamos ahora el producto interno (contracción) entre este tensor y el tensor dxq/dt:
Multiplicando para remover paréntesis:
Pero por la regla de la cadena, el primer término en el lado derecho de la ecuación es simplemente la derivada ordinaria de dAi/dt. Simplificando, llegamos a la relación que se quería demostrar desde un principio.
Para un tensor covariante , también podemos definir una derivada absoluta. La definición es casi idéntica a la dada anteriormente:
PROBLEMA: Partiendo del tensor covariante Ai, y formando el producto interno de la derivada covariante Ai, j con el vector tangente dxi/dt a una curva espacial, demostrar la siguiente relación:
La resolución de este problema se lleva a cabo en forma casi idéntica al problema anterior, la única diferencia siendo que utilizamos la derivada covariante para un tensor del tipo covariante en lugar de un tensor del tipo contravariante, lo cual se refleja en la diferencia de los signos del segundo término de la derivada absoluta de un tensor cuando se trata de un tensor covariante (-) y de un tensor contravariante (+).
Por una mera ligera conveniencia y sin ninguna otra razón más que esta, trabajaremos sobre la derivada absoluta de un tensor contravariante.
Si T = (Ti) es un tensor (contravariante), entonces la derivada (Ti, j) de dicho tensor (siguiendo las reglas para la derivada de un tensor con lo cual entran en el panorama los símbolos de Christoffel) también lo es. Supóngase que vamos a tomar el producto interno de este tensor T con otro tensor U = (dxi/dt) que viene el vector tangente a una curva espacial C cuyos i componentes (tres componentes en caso de un espacio tri-dimensional) son a su vez funciones de un parámetro t ( xi = xi(t) ):
Como ya lo vimos, a este producto se le designa como la derivada absoluta del tensor a lo largo de la curva espacial C siendo sus componentes:
Una cosa que debemos aquí es que en un sistema de coordenadas en los que los componentes del tensor métrico gij son constantes numéricas los símbolos de Christoffel se convierten todos en cero, con lo cual la diferenciación absoluta se nos reduce a lo que ya habíamos visto antes, a la derivada direccional de un vector. Lo que en el Análisis Vectorial llamamos derivada direccional en el Análisis Tensorial lo llamamos derivada absoluta, estando ambos conceptos siempre definidos a lo largo de una curva espacial, pero siendo siempre el concepto de la derivada absoluta más general y más extenso que el de la derivada direccional.
PROBLEMA: Demostrar que la diferenciación absoluta se convierte en diferenciación ordinaria: (1) en el caso del espacio tri-dimensional Euclideano manejado con coordenadas rectangulares Cartesianas, y (2) en el caso del espacio-tiempo Lorentziano (Minkoswki) que corresponde a la Teoría Especial de la Relatividad.
(1) En el caso del espacio tri-dimensional Euclideano manejado con coordenadas rectangulares Cartesianas, en donde el elemento de distancia ds está dado por:
ds² = dx² + dy² + dz²
los componentes del tensor métrico g son:
g11 = g22 = g33 = 1, y gij = 0 para i ≠ j
y por lo tanto todos los símbolos de Christoffel serán iguales a cero. Entonces:
se reduce a:
y la diferenciación absoluta se convierte en diferenciación ordinaria.
(2) En el caso del espacio-tiempo Lorentziano (Minkoswki) que corresponde a la Teoría Especial de la Relatividad, el elemento de distancia ds lo podemos escribir como:
ds² = c²dt² - dx² - dy² - dz²
con lo cual los componentes del tensor métrico g son:
g11 = 1, g22 = g33 = g44 = -1, y gij = 0 para i ≠ j
y por lo tanto todos los símbolos de Christoffel serán iguales a cero, produciéndonos el mismo resultado que la parte anterior.
Resulta obvio que todo lo que se ha definido arriba para un espacio tri-dimensional se puede extender sin problema alguno hacia un 4-espacio o inclusive a espacios de dimensiones mayores; y más aún, podemos llevarlo hacia espacios multidimensionales en donde hay curvatura a causa de un sistema de coordenadas en el que no todos los componentes del tensor métrico gij son constantes numéricas.
En un marco de referencia inercial (Lorentziano), toda la geometría Euclideana sigue siendo perfectamente válida. Las líneas paralelas permanecen paralelas. Del mismo modo, la suma de los ángulos internos de un triángulo cualquiera frente a un observador en reposo miden 180 grados:
y seguirán midiendo 180 grados cuando el triángulo se pone en movimiento a una velocidad constante frente al observador después de que todos los efectos relativistas han sido tomados en cuenta (las distancias paralelas a la dirección del movimiento se contraen mientras que las distancias perpendiculares permanecen iguales):
Sin embargo, si el triángulo es puesto en un marco de referencia acelerado, la suma de los ángulos internos del triángulo ya no será igual a 180 grados, e inclusive las líneas rectas del triángulo dejarán de ser líneas rectas, se volverán líneas curvas. La geometría dejará de ser Euclideana para convertirse en una geometría no-Euclideana.
Considérese ahora un plano Euclideano, sin curvatura alguna en la tercera dimensión espacial, en el cual se toma un vector V que está situado inicialmente en el punto A de un cuadrado y al cual se le arrastra mediante el procedimiento de transporte paralelo alrededor de los bordes del cuadrado, pasando por los puntos B, C y D hasta regresarlo al punto original de partida:
Después de completar de completar el recorrido completo ABCDA hasta volver al punto de origen, el vector arrastrado mediante el transporte paralelo continúa apuntando en la misma dirección que aquella a la que apuntaba al empezar el recorrido. Esto no ocurre en presencia de alguna curvatura, como en el caso en el cual se ha trazado un cuadrado como el de arriba muy grande sobre la superficie de una esfera. El transporte paralelo proporciona entonces una manera de poder determinar la curvatura de un espacio tridimensional o de un espacio-tiempo relativista. En un espacio-tiempo plano (Lorentziano) dV/dλ = 0. Vectorialmente hablando, esto significa que un vector V objeto de transporte paralelo no solo no cambia de magnitud al ser desplazado, ni siquiera cambia de dirección (sin embargo, en una región suficientemente pequeña, el espacio curvo se vuelve prácticamente plano. Esta aproximación nos permite considerar a un espacio-tiempo curvo formado por una cantidad enorme de “mosaicos” espacio-tiempo planos).
En el caso de un 4-espacio como el que se utiliza en la Teoría de la Relatividad, el vector tangente U se puede definir de la siguiente manera en función del parámetro τ a partir del vector posición x:
El parámetro es, desde luego, el tiempo propio τ medido por el reloj que viaja con el observador en movimiento.
Considérese ahora la siguiente curva espacial en la cual se han trazado vectores tangentes sobre dicha curva identificados como U y sobre la cual se ha tomado un vector V al cual se le ha aplicado el procedimiento de transporte paralelo:
Con la ayuda de la regla de la cadena podemos escribir lo siguiente tomándolo como algo matemáticamente válido (utilizamos derivadas ordinarias para cada dxi/dτ en virtud de que cada componente xi es función de una sola variable que es el parámetro τ, mientras que usamos derivadas parciales para las componentes ∂Vα/∂xi en virtud de que el vector V es una función no de una sino de varias variables xi):
Inspeccionando esto que acabamos de escribir, nos percatamos de que podemos representarlo de una manera más compacta como el producto interno (escalar) de un vector cuyas componentes son dxi/dτ por otro vector cuyas componentes son ∂Vα/∂xi. Esto lo podemos representar de dos maneras, ya sea en notación matricial (compacta o explícita) o recurriendo a notación de doble sumatoria usando índices repetidos. Optaremos aquí por esta última porque está más de cerca con el espíritu del tratamiento tensorial que se le dá a la Teoría de la Relatividad. Si repasamos lo que vimos arriba, no nos debe llevar mucho tiempo para darnos cuenta de que el vector cuyas componentes son dxi/dτ en realidad es el vector U = (Uβ) que es la tangente a la curva espacial. Esto significa que la expansión anterior la podemos representar de la manera siguiente:
Obsérvese que en la segunda línea hemos recurrido a la notación de la coma para representar la derivada parcial de Vα con respecto a xβ. Pero si repasamos lo que tenemos arriba, no tardamos en caer en la cuenta de que lo que tenemos en UβVα,β es esencialmente la definición de la derivada absoluta del tensor (vector) V. Pero si como vimos arriba, en un espacio-tiempo plano (Lorentziano) dV/dλ = 0, entonces el enunciado siguiente:
Uβ Vα , β = 0
es esencialmente la definición del transporte paralelo del vector V a lo largo del vector tangente U trazado sobre la curva espacial. Pero esta es una expresión tensorial, válida en cualquier marco de referencia. Por lo tanto, aplicando la regla de “la coma va hacia un semicolon”, reemplazando con ello a la derivada ordinaria con la derivada covariante (la cual involucra ya a los símbolos de Christoffel), tenemos entonces la siguiente expresión:
Uβ Vα ; β = 0
Esta es la definición invariante (válida para cualquier marco de referencia) del transporte paralelo del vector V a lo largo del vector tangente U. En otras palabras, si UβVα,β = 0 entonces dV/dλ = 0, y viceversa. La definición invariante del transporte paralelo es a veces presentada de manera algo críptica aunque compacta de la siguiente manera:
cuyo lado izquierdo se acostumbra leer como “la derivada covariante de V tomada a lo largo del vector tangente U”. Este es otro caso de una selección desafortunada de simbología, puesto que el operador diferencial vectorial nabla ∇ nunca se aplica directamente sobre un vector, se aplica sobre un campo escalar transformando a dicho campo escalar en un campo vectorial, del mismo modo que en manipulaciones matemáticas no se acostumbra anexarle sub-índices a dicho operador, y mucho menos sub-índices vectoriales.
Regresando al espacio plano, tenemos en él las líneas más importantes que se puedan trazar en dicho espacio, que son las líneas rectas. Un postulado básico de la geometría Euclideana nos dice que dos rectas paralelas que son inicialmente paralelas permanecerán paralelas cuando son prolongadas. Esto no significa que podamos utilizar a la distancia que haya entre dos líneas para determinar si son paralelas cuando son continuadas, porque ambas líneas pueden experimentar una curvatura manteniéndose la distancia entre ambas constante (como lo que ocurre en las carreteras en donde al tomar una curva la distancia entre ambos lados de la carretera permanece más o menos constante). Lo que significa el que dos rectas permanezcan paralelas cuando son continuadas es que ambas permanezcan moviéndose siempre en una misma dirección, de modo tal que la tangente a una línea sea paralela a la tangente trazada sobre la misma línea en un punto previo o posterior. De hecho, la línea recta es la única curva en el espacio Euclideano capaz de llevar a cabo un transporte paralelo sobre su propio vector tangente. En un espacio curvo también podemos trazar líneas “tan derechas como sea posible” demandando el transporte paralelo del mismo vector tangente. Estas líneas ya las vimos en las entradas previas. Son las geodésicas. Recuérdese cómo habíamos definido a las geodésicas como “las líneas más derechas posibles entre dos puntos cualesquiera”. Simbólicamente, este requerimiento matemático para tener “líneas tan derechas como sea posible” se puede representar de la siguiente manera:
Utilizando notación de componentes, lo anterior se puede expresar de la siguiente manera en forma menos críptica y más susceptible a la manipulación matemática haciendo V = U en la definición invariante del transporte paralelo del vector V a lo largo del vector tangente U:
Uβ Uα ; β = 0
Aplicando la definición de la derivada covariante como nos lo pide el semicolon (metiendo dentro del panorama a los símbolos de Christoffel), y manteniéndonos dentro de la notación de componentes, lo anterior se nos convierte en:
UβUα,β + Γαμβ UμUβ = 0
Si identificamos a λ como un parámetro medido a lo largo de la curva (ya sea un elemento de arco o un elemento de tiempo propio medido por un observador que viaja con su reloj a lo largo de la curva) de modo tal que el vector tangente pueda ser escrito como Uα = dxα/dλ; esto puede ser simplificado aún más, pero para ello necesitamos probar el siguiente resultado intermedio:
Uβ · ∂/∂xβ = d/dλ
Puesto que, de un paso previo:
dVα/dλ = Uβ Vα , β
entonces:
de lo cual se infiere que:
Tenemos además que:
Es así como llegamos al siguiente sistema de ecuaciones:
O bien:
Esto último tiene ya un aspecto que nos debe resultar familiar. Es la ecuación geodésica que ya habíamos obtenido anteriormente por medio del cálculo de variaciones recurriendo a la ecuación de Euler, y que hemos obtenido ahora aquí mediante argumentos de índole física. Como podemos constatar, la ruta geodésica, el transporte paralelo y la curvatura del espacio-tiempo son conceptos que están íntimamente ligados.