Armados con las transformaciones de Lorentz podemos, sin perder tiempo en los detalles de casos particulares, obtener resultados generales como el que logramos en respuesta al siguiente
PROBLEMA: ¿Cuál será la forma en un marco de referencia S’ de un pulso esférico luminoso obtenido al hacer estallar un petardo en el marco de referencia S?
En un sistema de coordenadas Cartesianas en tres dimensiones (x,y,z) puesto en el marco de referencia S, la ecuación de una esfera de radio r centrada en el origen estará dada por:
x² + y² + z² = r²
Si en el marco de referencia S hacemos estallar un petardo obteniendo con ello una esfera de luz en torno al petardo que actúa como el centro de dicha esfera, dicha esfera se irá expandiendo conforme avanza el tiempo, y el radio de la misma será r = ct. Entonces, para el pulso luminoso esférico en el marco de referencia S, tenemos:
x² + y² + z² = c²t²
La forma de dicho pulso esférico luminoso estará dada en el marco de referencia S’ por lo que dictan las transformaciones de Lorentz:
x = γ(x’ - vt’)
y = y’
z = z’
t = γ(t’ - Vx’/c²)
y = y’
z = z’
t = γ(t’ - Vx’/c²)
Substituyendo estas ecuaciones de transformación en la ecuación del pulso esférico luminoso, tras un poco de álgebra laboriosa obtenemos lo siguiente para el pulso esférico luminoso en el marco de referencia S’:
(x’)² + (y’)² + (z’)² = c²(t’)²
Pero esta es también la ecuación de una esfera luminosa dentro del marco de referencia S’.
Un pulso esférico luminoso en un marco de referencia S tendrá también la misma forma esférica en otro marco de referencia S’ que se está moviendo a una velocidad V con respecto a S.
El que la forma geométrica de un pulso esférico luminoso sea la misma independientemente del marco de referencia en el que estemos situados, invariante, nos hace concebir la posibilidad de que también pueda haber otras invariantes que no cambien de un marco de referencia a otro. Esto nos lleva al estudio de algo que en la Teoría Especial de la Relatividad se conoce como el intervalo.
Por convención, el intervalo relativista entre dos eventos distintos A y B se define de la manera siguiente:
Δs² = (cΔt)² - (Δx)² - (Δy)² - (Δz)²
Δs² = (ctB - ctA)² - (xB - xA)² - (yB - yA)² - (zB - zA)²
A continuación haremos un ejercicio llevando a cabo el cálculo del intervalo relativista entre dos eventos A y B. Para este ejemplo, las coordenadas cuatri-dimensionales del evento A serán:
(ctA = 5.0 m, xA = 3.0 m, yA = 2 m, zA = 0.0 m )
Y para el evento b las coordenadas cuatri-dimensionales serán:
(ctB = 6.0 m, xB = 3.0 m, yB = 2.5 m, zB = 0.0 m )
El intervalo relativista será entonces:
Δs² = (ctB - ctA)² - (xB - xA)² - (yB - yA)² - (zB - zA)²
Δs² = ( 6.0 m - 5.0 m)² - (3.0 m - 3.0 m)² -(2.5 m - 3.0 m)² - ( 0.0 m - 0.0 m)²
Δs² = 1.0 m² - 0.0 m² - (-0.5 m)² - 0.0 m² = 0.75 m²
Δs² = ( 6.0 m - 5.0 m)² - (3.0 m - 3.0 m)² -(2.5 m - 3.0 m)² - ( 0.0 m - 0.0 m)²
Δs² = 1.0 m² - 0.0 m² - (-0.5 m)² - 0.0 m² = 0.75 m²
Podemos tomar la raíz cuadrada si así lo deseamos para obtener:
Δs = 0.87 m.
Sin embargo, esto no es lo que se acostumbra hacer en los estudios de la Teoría Especial de la Relatividad. El estudiante para el que todo esto es nuevo se debería de acostumbrar a considerar a Δs² como un solo símbolo y no como el cuadrado de una cantidad Δs. Puesto que Δs² puede ser una cantidad positiva o negativa, no es conveniente tomar la raíz cuadrada. Debe ser claro también que la notación Δs² NO significa Δ(s²), y por ello es preferible acostumbrarse a leerla como un solo símbolo.
A continuación veremos un problema que nos confirmará que el intervalo es una cantidad invariante que no cambia al pasar de un marco de referencia a otro.
PROBLEMA: Usando las transformaciones de Lorentz, encontrar las coordenadas (x,t) que corresponden en el sistema S’ al evento E1 cuyas coordenadas son (x’,t’) = (2,5) si la velocidad relativa entre ambos marcos de referencia es V = 0.6 metros/segundo. A continuación, repetir los cálculos para el evento E2 cuyas coordenadas son (x,t) = (2,5). Hecho esto, comprobar que el intervalo Δs² entre los eventos E1 (x,t) y E2(x,t) tiene el mismo valor que el intervalo (Δs’)² entre los eventos E1 (x’,t’) y E2(x’,t’).
En este caso:
γ = 1/√1 - V²/c² = 1/√1 - (0.6 m/seg)²/(1 m/seg)²
γ = 1/√1 - 0.36 = 1/√0.64 = 1/0.8
γ = 1.25
γ = 1/√1 - 0.36 = 1/√0.64 = 1/0.8
γ = 1.25
A continuación recurrimos a las transformaciones de Lorentz:
x = γ(x’ + Vt’)
x = (1.25) [2 + (0.6)(5)] = (1.25)(5)
x = 6.25
t = γ(t’ + Vx’/c²)
t = (1.25) [5 + (0.6)(2)]
t = 7.75
x = (1.25) [2 + (0.6)(5)] = (1.25)(5)
x = 6.25
t = γ(t’ + Vx’/c²)
t = (1.25) [5 + (0.6)(2)]
t = 7.75
Entonces tenemos lo siguiente:
E1 (x,t) = (6.25, 7.75)
E1 (x’,t’) = (2, 5)
E1 (x’,t’) = (2, 5)
Obsérvese que no usamos la comilla para denotar E1 (x’,t’) como E1’ porque se trata del mismo evento. Lo único que cambian son sus coordenadas al pasar de un marco de referencia a otro.
Usando nuevamente las transformaciones de Lorentz, para el evento E2 cuyas coordenadas en S’ son (x’,t’) = (3, 10), sus coordenadas en S serán:
x = (1.25) [3 + (0.6)(10) ] = 11.25
t = (1.25) [10 + (0.6)(3) ] = 14.75
t = (1.25) [10 + (0.6)(3) ] = 14.75
El cálculo del intervalo Δs² entre los dos eventos E1 y E2 en el marco de referencia S arroja lo siguiente:
Δs² = (cΔt)² - (Δx)²
Δs² = (14.75 - 7-75)² - (11.25 -6.25)²
Δs² = 24
Δs² = 24
Por otro lado, el cálculo del intervalo (Δs’)² entre los dos eventos E1 y E2 en el marco de referencia S’ arroja lo siguiente:
(Δs’)² = (cΔt)² - (Δx)²
(Δs’)² = (10 - 5)² - (3 - 2)²
(Δs’)² = (10 - 5)² - (3 - 2)²
(Δs’)² = 24
Con esto se concluye que:
Δs² = (Δs’)²
Se verifica aquí que el intervalo entre dos eventos es una invariante al pasar de un marco de referencia a otro.
Para demostrar lo anterior en el caso general, sin recurrir a números, simplemente repetimos lo que hicimos en la resolución del problema numérico, usando símbolos. La diferencia entre dos eventos E1 y E2 en S está dada por:
Δs² = (cΔt)² - (Δx)²
Δs² = c²(t2-t1)² - (x2 - x1)²
Δs² = c²(t2-t1)² - (x2 - x1)²
Usamos ahora las transformaciones de Lorentz:
t1 = γ(t’1 + Vx’1/c²)
t2 = γ(t’2 + Vx’2/c²)
x1 = γ(x’1 + Vt’1)
x2 = γ(x’2 + Vt’2)
t2 = γ(t’2 + Vx’2/c²)
x1 = γ(x’1 + Vt’1)
x2 = γ(x’2 + Vt’2)
Sustituyendo estas cuatro relaciones en la relación anterior y simplificando y reduciendo lo más posible, obtenemos:
Δs² = (ct’2 - ct’1)² - (x’2 - x’1)²
Δs² = (cΔt’)² - (Δx’)²
Δs² = (Δs’)²
Δs² = (Δs’)²
En todo intervalo relativístico identificamos dos partes claramente distiguibles, el componente espacial:
(Δx)² - (Δy)² - (Δz)²
y el componente temporal:
(cΔt)²
Cuando en un intervalo relativista entre dos eventos predomina el componente temporal sobre el componente espacial, lo llamamos un intervalo tipo temporal (timelike). Cuando en un intervalo relativista predomina el componente espacial sobre el componente temporal, lo llamamos intervalo tipo espacial (spacelike). Y cuando en un intervalo relativista el componente espacial es igual al componente temporal (en cuyo caso el intervalo será igual a cero) se le conoce como intervalo tipo luminoso (lightlike) o intervalo nulo (null).
PROBLEMA: Para los pares de eventos cuyas coordenadas (ct, x, y, z) en algún marco de referencia son las que se dan a continuación, clasificar la separación entre cada par de eventos como tipo temporal, tipo espacial, o tipo luminoso.
a) (0,0,0,0) y (-1,1,0,0)
b) (1,1,-1,0) y (-1,1,0,2)
c) (6,0,1,0) y (5,0,1,0)
d) (-1,1,-1,1) y (4,1,-1,6)
a) (0 -(-1))² - (0 - 1)² - (0 - 0)² - (0 - 0)² = 1 - 1
Puesto que la parte temporal es igual a la parte espacial, la separación es tipo luminoso.
b) (1 -(-1))² - (1 - 1)² - (-1 - 0)² - (0 - 2)² = 4 - 5
Puesto que la parte espacial es mayor que la parte temporal, la separación es tipo espacial.
c) (6 -5)² - (0 - 0)² - (1 - 1)² - (0 - 0)² = 1 - 0
Puesto que la parte temporal es mayor que la parte espacial, la separación es tipo temporal.
d) (-1 -4)² - (1 - 1)² - (-1 - (-1))² - (1 - 6)² = 25 - 25
Puesto que la parte temporal es igual a la parte espacial, la separación es tipo luminoso.
Si prescindimos de los símbolos Δ por sobreentenderse y designamos a x²+y²+z² simplemente como r², el intervalo s² se puede simbolizar como:
s² = (ct)² - r²
y en un diagrama espacio-tiempo tenemos entonces tres regiones distinguibles:
El origen en el diagrama espacio-tiempo (ct, r) = (0, 0) representa el “ahora”. En la región de color amarillo que representa el “futuro” que le espera al observador predomina el componente temporal sobre el componente espacial, con lo cual s² siempre es mayor que cero (positivo) y por lo tanto es una región de intervalos tipo temporal (timelike). En la región de color ciano que representa el “pasado” que recorrió el observador también predomina el componente temporal sobre el componente espacial, con lo cual s² siempre es mayor que cero (positivo) y por lo tanto también es una región de intervalos tipo temporal (timelike). En las líneas que delimitan al cono de luz la componente temporal es igual a la componente espacial con lo cual s² = 0, y es aquí en donde tenemos a los intervalos tipo luminoso que involucran rayos de luz. Y fuera de todo esto tenemos a los intervalos en donde el componente espacial es mayor que el componente temporal con lo cual s² es menor que cero (negativo) siendo por lo tanto la región de intervalos tipo espacial (spacelike).
La definición que se ha dado arriba para el intervalo relativista no es universal. Aunque es muy utilizada, muchos otros textos lo definen usando una convención inversa de signos:
Δs² = - (cΔt)² + (Δx)² + (Δy)² + (Δz)²
De cualquier manera, las definiciones que se han dado arriba para el intervalo tipo espacial, el intervalo tipo temporal, y el intervalo tipo luminoso, no cambian en lo absoluto, ya que en dichas definiciones lo que cuenta es la predominancia de un componente sobre el otro. Sin embargo, es necesario hacer esta aclaración porque mientras que en textos sobre la relatividad como el de David W. Hogg el intervalo es considerado como un intervalo tipo espacial si Δs² es menor que cero (negativo), en otros libros como el de Kip Thorne la situación es al revés y el intervalo es considerado como un intervalo tipo espacial si Δs² es mayor que cero (positivo), siendo la diferencia ocasionada por la forma en la cual se ha definido a Δs².
Al tratar sobre el tema de “Los diagramas espacio-tiempo de Minkowski” en donde estudiamos la Teoría Especial de la Relatividad desde una perspectiva geométrica, había quedado un asunto pendiente, el asunto de graduar o calibrar tanto los ejes coordenados del observador en reposo O como del observador en movimiento O de modo tal que los diagramas espacio-tiempo se pudieran utilizar para una resolución de problemas un poco más cuantitativa que cualitativa. Esto lo podemos llevar a cabo, también geométricamente, utilizando lo que se conoce como la hipérbola invariante.
Primero que nada, haremos un repaso de lo que es la hipérbola de acuerdo con la Geometría Analítica.
Una hipérbola es el lugar de los puntos tales que la diferencia de las distancias de cada uno de ellos a dos puntos fijos es constante. La hipérbola está dada por una ecuación como la siguiente:
y² - x² = C²
en donde C es una constante numérica y cuya gráfica tiene el siguiente aspecto para C = 1:
Sin necesidad de tener que hacer cálculos numéricos, tal como lo hacían los griegos en la antigüedad (los cuales no conocían el álgebra y mucho menos la geometría analítica) podemos construír geométricamente la hipérbola mostrada arriba con un simple compás con el procedimiento que será dado a continuación. Primero localizamos sobre el eje-y dos puntos A y B que estén ubicados ambos a una distancia de 2 unidades del origen, o sea en los puntos A(0,2) y B(0,-2):
A continuación, empezamos a trazar una curva de modo tal que para cualquier punto P de la curva la diferencia entre la distancia del punto P al punto A (PA) y del punto P al punto B (PB) sea igual a una constante de 2 unidades, o sea:
PB - PA = 2
Si continuamos adelante con nuestro procedimiento de construcción, iremos obteniendo una curva como la siguiente:
Aplicando el mismo procedimiento podemos construír la parte correspondiente al lado izquierdo de la curva. Una vez que hemos completado la construcción de la curva superior, podemos llevar a cabo la construcción de la parte inferior:
Para la curva inferior tenemos:
PA - PB = 2
Es importante destacar que una hipérbola en realidad son dos curvas, las curvas que tenemos en el diagrama de arriba. En sus extremos, ambas curvas casi toman la forma de líneas rectas, conocidas como las asíntotas.
Hay también otra hipérbola, la cual está dada por la siguiente ecuación:
x² - y² = C²
y cuya gráfica es la siguiente (el procedimiento de construcción es el mismo que el anterior):
Si reescribimos la ecuación de la hipérbola
y² - x² = C²
hacemos el siguiente cambio de notación:
(cΔt)² - (Δx)² = Δs²
Δs² = (cΔt)² - (Δx)²
Δs² = (cΔt)² - (Δx)²
esto lo reconocemos inmediatamente como un intervalo relativista. El intervalo no es solo una invariante de un marco de referencia a otro. Graficado sobre un diagrama espacio-tiempo resulta ser una hipérbola equilátera, conocida como la hipérbola invariante, la cual podemos trazar directamente sobre el diagrama espacio-tiempo.
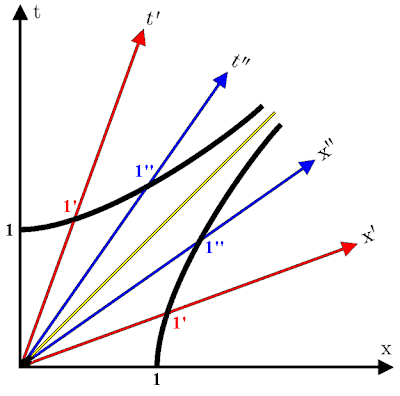
El hecho de que toda la curva hiperbólica represente una invariante de un marco de referencia a otro nos permite llevar a cabo algo que había quedado pendiente en la entrada “Los diagramas espacio-tiempo de Minkowski” en la construcción del diagrama espacio-tiempo: la calibración de los ejes de las coordenadas (x’,t’). Teniendo ya graduados con divisiones iguales los ejes horizontal y vertical del diagrama espacio-tiempo correspondiente al observador estacionario O en el marco de referencia S, nos basta con construír hipérbolas para llevar las graduaciones respectivas a los dos ejes coordenados del observador O’. De este modo, en el siguiente diagrama, la graduación del punto 1 es llevada al punto 1’ del marco de referencia de O’, y es llevada al punto 1’’ del marco de referencia del observador O’’ que se mueve a una velocidad aún más cercana a la velocidad de la luz, y así sucesivamente:
De este modo así es como llegamos a tener la siguiente graduación de ejes:
A continuación tenemos la siguiente hipérbola invariante sobre la cual se han llevado a cabo algunos cálculos numéricos sobre el intervalo relativista AB para un objeto que se desplaza del punto B al punto A:
Y a continuación tenemos un ejemplo de una serie completa de hipérbolas equiláteras que se han construído sobre escalas graduadas:
Estamos ahora en una posición que nos permite explicar la naturaleza del intervalo relativista como una invariante. Cuando dos naves espaciales pasan la una frente a la otra moviéndose a gran velocidad en direcciones contrarias, los viajeros de cada nave verán ciertos cambios en la apariencia de la otra nave así como cambios en el comportamiento de los relojes de la otra nave. Esto se debe a que el espacio y el tiempo no son absolutos que tengan una existencia independiente el uno del otro. Son, por así decirlo, proyecciones de sombras de un objeto cuatri-dimensional, del mismo modo que la sombra de un cubo nos muestra únicamente una imagen en dos dimensiones de algo que en realidad tiene una existencia en tres dimensiones:
Si vemos un invernadero por arriba, por el frente, y por uno de sus lados:
resulta obvio que mientras que la vista desde arriba parece mostrarnos un objeto rectangular delgado, al movernos hacia abajo la vista de lado parece mostrarnos un objeto menos rectangular, menos delgado. El objeto en sí no cambia de forma ni de tamaño, lo único que cambia es la proyección de su sombra hacia un plano de dos dimensiones. De la misma manera, en relatividad lo que un observador aprecia es un objeto de cuatro dimensiones, como en el caso de los viajeros en las dos naves espaciales, los cuales ven proyecciones tri-dimensionales diferentes de un mismo objeto dependiendo de su movimiento relativo en relación a dicho objeto. En algunos casos, la proyección de la sombra muestra más de tiempo que de espacio, y en otros casos muestra más de espacio que de tiempo. Los cambios que un viajero en una de las naves observa en las dimensiones de espacio y de tiempo de la otra nave pueden ser explicados como una especie de “rotación” en el espacio-tiempo, la cual ocasiona que se alteren las proyecciones de las sombras arrojadas por el espacio y el tiempo. Esto es precisamente lo que tenía en mente Hermann Minkowski, el creador de los diagramas de espacio-tiempo, cuando señaló el 21 de septiembre de 1908 en su discurso de inauguración de la 80ava reunión de la Asamblea General Alemana de científicos naturales y físicos: “Las ideas sobre el espacio y el tiempo que deseo mostrarles hoy descansan en el suelo firme de la física experimental, en la cual yace su fuerza. Son ideas radicales. De aquí en delante, el espacio y el tiempo por separado están destinados a desvanecerse como meras sombras, y tan sólo una unión de ambos puede preservar una realidad independiente”. Y esta idea la podemos ver reflejada claramente en un diagrama espacio-tiempo de Minkowski que muestra el intervalo entre dos eventos A y B:
En este diagrama espacio-tiempo tenemos el privilegio de ver un intervalo cuatri-dimensional AB cuya sombra proyectada sobre el espacio del observador O en el eje X (de color verde) tiene una magnitud diferente de su sombra proyectada sobre el espacio del observador O’ en el eje X’ (de color ciano), y cuya sombra proyectada sobre el tiempo del observador O en el eje ct (de color verde) tiene una magnitud diferente de su sombra proyectada sobre el tiempo del observador O en el eje ct’ (de color ciano), pero nosotros que lo estamos viendo “desde arriba” lo vemos tal como es.
Lo importante a captar aquí es el hecho de que la estructura espacio-tiempo, la estructura cuatri-dimensional de un objeto tal como una nave espacial, es algo tan rígido como lo era en la física clásica tri-dimensional. Esta es la diferencia esencial entre la teoría de la contracción de Lorentz-Fitzgerald ocasionada sobre los objetos físicos al moverse en el espacio venciendo la resistencia del supuesto éter, y la contracción Einsteniana. Para Lorentz, la contracción era una contracción real de un objeto tri-dimensional, mientras que para Einstein el objeto “real” es un objeto cuatri-dimensional que no cambia en lo absoluto, un objeto que cuyos cambios aparentes se deben a que es visto desde diferentes ángulos. Su proyección tri-dimensional en el espacio y su proyección uni-dimensional en el tiempo pueden cambiar, pero el objeto cuatri-dimensional del espacio-tiempo no cambia en nada. De este modo, el intervalo cuatri-dimensional entre dos eventos en el espacio-tiempo es un intervalo absoluto, invariante. Dos observadores distintos moviéndose el uno con respecto al otro a grandes velocidades estarán en desacuerdo sobre qué tan separados estarán dos eventos en el espacio, o qué tan separados estarán los dos eventos en el tiempo, pero dos observadores diferentes siempre estarán en total acuerdo sobre qué tan separados están dos eventos en el espacio-tiempo. En su libro “Spacetime Physics”, E. F. Taylor y J. A. Wheeler lo ponen de la siguiente manera: “El espacio es diferente para dos observadores distintos. El tiempo es diferente para dos observadores distintos. Pero el espacio-tiempo es el mismo para todos”.
Desde una perspectiva más formal, podríamos preguntarnos: ¿por qué el intervalo relativista es una cantidad que permanece inalterable de un marco de referencia a otro?
Para responder a esta última pregunta, haremos un repaso sobre la interpretación física y geométrica que les damos a las cantidades conocidas como los escalares y los vectores.
Los escalares son cantidades tales como la temperatura de un cuerpo o el color de una esmeralda. Tales cantidades no tienen dirección alguna que se les pueda asignar, y son cantidades que permanecen invariables sin cambiar en lo absoluto cuando se cambia de un marco de referencia a otro.
En cambio los vectores representan cantidades que apuntan definitivamente en cierta dirección, como la dirección en la cual está soplando el viento o como la dirección en la cual se está moviendo la Luna en un momento dado al girar en torno a la Tierra. Esta es la razón por la cual frecuentemente se representan en los pizarrones con una flechita puesta encima de ellos.
Un objeto que se está moviendo en línea recta en la dirección del eje de las equis (en un plano Cartesiano x-y) puede ser representado como una flecha apuntando en una dirección específica (+x) en la cual su vector velocidad tiene cierta longitud que se representará de mayor magnitud cuanto mayor sea la velocidad del objeto. Supóngase para fines de demonstración numérica que se trata de un avión moviéndose hacia la derecha a una velocidad de 50 metros por segundo.
Ahora bien, si le damos al vector velocidad una rotación con respecto al origen, la magnitud del vector no cambiará, lo que cambiarán serán las componentes utilizadas para especificarlo. Es así como podemos tener un vector en dos dimensiones como el siguiente:
Podemos imaginar al avión representado por la línea m moviéndose en dirección Norte-Este a una velocidad de 5 metros por segundo. La magnitud de la velocidad sigue siendo la misma, pero su dirección ha cambiado. Podemos imaginar que su velocidad horizontal ha disminuído a 3 metros por segundo pero que un viento que está soplando de Sur a Norte lo está empujando a una velocidad de 4 metros por segundo. Por el teorema de Pitágoras, la magnitud de la velocidad es de 5 metros por segundo. La velocidad total tiene dos componentes, una componente horizontal de 3 metros por segundo y una componente vertical de 4 metros por segundo.
No hay razón alguna por la cual tengamos que limitar a nuestro vector a un espacio bidimensional. Podemos imprimirle otra rotación adicional para situarlo en un espacio tridimensional. El vector velocidad de esta manera estará especificado por tres componentes, las cuales requieren de tres planos diferentes, ortogonales (situados a ángulos rectos el uno del otro) entre sí:
para poder especificar a nuestro vector tridimensional mediante tres componentes, siendo cada componente la proyección del vector sobre cada uno de los planos:

De este modo, podemos especificar nuestro vector en un plano Cartesiano tridimensional de una manera como la siguiente:
Representamos la descomposición del vector A en tres componentes como un triplete ordenado:
A = ( ax , ay , az )
Nuevamente, la longitud del vector sigue siendo la misma, lo único que ha cambiado es su representación en un espacio tridimensional en vez de un espacio bidimensional.
Ahora viene un salto que al principio requiere algo de fé. Supondremos la existencia de un espacio en cuatro dimensiones, y que el vector que hemos estado considerando de alguna manera puede ser girado (rotado) de modo tal que el vector tenga ahora proyecciones sobre cada una de estas cuatro dimensiones. El vector ahora tendrá cuatro componentes que podemos escribir como una cuadrupla ordenada:
A = ( a1 , a2 , a3 , a4 )
Geométricamente hablando, nos es imposible poder visualizar un espacio de cuatro dimensiones porque nuestros cerebros están “alambrados” para trabajar y pensar en tres dimensiones. Pero, matemáticamente hablando, no hay nada que nos impida hacer tal descomposición de nuestro vector en cuatro componentes bajo la condición de que la longitud del vector siga permaneciendo la misma. La longitud del vector, en efecto, debe permanecer invariante en todo momento.
La pregunta ahora es: ¿cómo podemos evaluar la longitud de un vector cuando ese vector está especificado en un espacio de cuatro dimensiones?
La respuesta obvia consiste en tratar de extender el teorema de Pitágoras hacia un espacio de varias dimensiones, empezando con lo que ya se tiene y se sabe que es cierto. En un plano de dos dimensiones, el teorema de Pitágoras que nos permite obtener la longitud d de un vector trazado en un plano nos dice que para todo triángulo rectángulo el cuadrado de la hipotenusa c es igual a la suma de los cuadrados de los catetos a y b:
d² = a² + b²
De este modo, la longitud del vector, que es invariable porque es un escalar, se obtiene simplemente sacando la raíz cuadrada de ambos lados:
¿Y cómo obtenemos la longitud de un vector tridimensional como el siguiente, en el cual no parece haber un triángulo con dos catetos?:
Lo podemos hacer de la siguiente manera. Primero obtenemos la longitud L de la hipotenusa del triángulo rectángulo formado por los catetos a y b:
Por el teorema de Pitágoras en dos dimensiones, sabemos que:
L² = a² + b²
Una inspección al diagrama nos revela que el lado L es a su vez el cateto de otro triángulo rectángulo formado por los catetos L y c:
Para este triángulo rectángulo plano, la aplicación del teorema de Pitágoras nuevamente nos dá:
d² = L² + c²
Pero puesto que L² = a² + b², tenemos entonces que la longitud de un vector tridimensional cuyas componentes en los tres ejes son a, b y c está dada por la fórmula:
Este es esencialmente el teorema de Pitágoras en tres dimensiones. El mismo procedimiento que hemos llevado a cabo aquí lo podemos utilizar para ir extendiendo la fórmula del teorema de Pitágoras hacia un espacio de cuatro dimensiones, aunque no nos sea posible visualizarlo, e inclusive la podemos ir extendiendo hacia un espacio n-dimensional con cualquier cantidad n de dimensiones.
Para un vector V cuyas tres componentes están dadas por el triplete (a, b, c), la cantidad la podemos representar de la siguiente manera como el producto de los componentes respectivos del vector con los cuales obtenemos la longitud del vector:
a² + b² + c² = a·a + b·b + c·c
a² + b² + c² = d·d
a² + b² + c² = d·d
Esta es precisamente la forma en la cual obtenemos la longitud de un vector, más formalmente (y más pomposamente) conocida como la norma de un vector; multiplicando los componentes rectangulares respectivos, sumándolos y extrayendo la raíz cuadrada. La longitud de un vector en n dimensiones cuyas componentes sean x1 , x2 , x3 ... xn estará dada por:
En un espacio de cuatro dimensiones, como el que tenemos en la Teoría Especial de la Relatividad en donde la cuarta dimensión está especificada por la longitud obtenida al multiplicar la constante c (la velocidad de la luz) por la variable tiempo, la longitud de un vector cuatri-dimensional es invariable por ser una magnitud escalar, y en este caso el vector que une a dos eventos diferentes E1 y E2 en ese espacio de cuatro dimensiones también tendrá la misma longitud al darle una rotación en algún sentido al cambiar de un marco de referencia a otro. Esta es la razón del por qué el intervalo relativista es una cantidad invariable, porque se trata de una longitud (o mejor dicho, el cuadrado de una longitud), se trata de un escalar.
El teorema de Pitágoras extendido a cinco dimensiones nos diría “el cuadrado de la hipotenusa d de un triángulo rectángulo concebido en cinco dimensiones es igual a la suma de los cuadrados de los cinco “catetos” adyacentes a, b, c, d y e a la hipotenusa”:
d² = a² + b² + c² + d² + e²
Este es el teorema de Pitágoras extendido a cinco dimensiones. Ahora bien, si definimos una “distancia” s² en cuatro dimensiones de la siguiente manera:
s² = a² - b² - c² - d²
el lector podrá objetar diciendo que esto ya no es el teorema de Pitágoras, a causa de la introducción de los signos negativos reemplazando a los signos positivos, máxime que esta definición abre la posibilidad de que la “distancia” s² sea cero pese a que ninguno de los componentes a, b, c y d sean cero. Sin embargo, aunque esto no sea ya el teorema de Pitágoras “clásico”, esta es una definición perfectamente válida de “distancia”. Esta selección de signos nos ha proporcionado ya una cantidad invariable, el intervalo relativista. Lo que hemos definido, más que una distancia clásica, es una métrica. La métrica contiene toda la información que necesitamos conocer para poder describir lo que sucede tanto en la Teoría Especial de la Relatividad como en la Teoría General de la Relatividad. Y al ir ajustando nuestra manera de pensar nos estamos preparando mentalmente para dar el gran salto hacia los marcos de referencia acelerados que estaban proscritos dentro de la Teoría Especial de la Relatividad.
La razón por la cual en la Teoría de la Relatividad no nos resulta de utilidad alguna definir una distancia al “estilo” del teorema de Pitágoras como la siguiente, usando únicamente signos positivos:
(cΔt)² + (Δx)² + (Δy)² + (Δz)²
es porque no resulta difícil comprobar que ésta cantidad no es una invariante bajo las transformaciones de Lorentz, aunque se trate de una cantidad escalar. El primer requisito fundamental que toda métrica debe cumplir es que debe ser capaz de producir un intervalo invariante al llevarse a cabo un cambio de coordenadas.
Podemos representar de una manera más elegante (y mucho más útil) las componentes x1 , x2 , x3 y x4 de un vector cuatri-dimensional ya sea como un vector renglón:
[ x1 _x2 _x3 _x4]
o como un vector columna (al cual en matemáticas se le llama transpuesta):
Estas dos definiciones nos permiten representar a la cantidad escalar:
a·b = a1b1 + a2b2 + a3b3
como el producto matricial:
y, mucho más importante, representar a la cantidad escalar:
(cΔt)² - (Δx)² - (Δy)² - (Δz)²
como el producto de tres matrices:
El núcleo del asunto, lo verdaderamente importante, radica en la matriz intermedia, puesto que esta matriz es precisamente la matriz que nos define a la métrica, a la cual podemos llamar matriz métrica. Es precisamente esta matriz la que nos proporciona el intervalo relativista que permanece invariante bajo las transformaciones de Lorentz. Es precisamente esta matriz la que nos define un espacio-tiempo plano, Euclideano, en el cual se cumple el quinto postulado de Euclides que nos dice que “dos rectas paralelas nunca se cruzan ni divergen separándose la una de la otra” (como las líneas del mundo de los extremos de una vara de medir que está reposo y las cuales nunca se cruzan ni se separan en un diagrama espacio-tiempo). Y será esta matriz la que, con una selección diferente en sus 16 componentes, nos definirá un espacio-tiempo curvo en el que no se cumple el quinto postulado de Euclides.
En la Teoría General de la Relatividad en donde los observadores ya no se mueven en línea recta a una velocidad constante el uno con respecto al otro, no nos es posible seguir considerando simples diferencias lineares Δ entre las coordenadas por no mantenerse constantes dichas diferencias de un punto a otro. Tenemos que considerar intervalos relativísticos infinitesimales. Así, en vez de usar la distancia
(cΔt)² - (Δx)² - (Δy)² - (Δz)²
tenemos que usar el intervalo relativista infinitesimal
(cdt)² - (dx)² - (dy)² - (dz)²
Este intervalo relativista es el intervalo que corresponde a un espacio-tiempo plano, un espacio-tiempo Minkowski o Lorentziano. Generalmente hablando, el intervalo que corresponde a un espacio-tiempo curvo como el que se estudia en la Teoría General de la Relatividad tiene una métrica como la siguiente:
g0(cdt)² - g1(dx)² - g2(dy)² - g3(dz)²
Como un anticipo de lo que nos espera en la Teoría General de la Relatividad, y como nuestro primer contacto con un espacio-tiempo curvo, a continuación tenemos lo que se conoce como la métrica de Schwarzchild:
ds² = (1 - 2GM/rc²)(cdt)² - (1 - 2GM/rc²) -1(dr)² - (r²)(dθ)²
- (r² sen² θ)(dφ)²
- (r² sen² θ)(dφ)²
(Tómese nota de que, a diferencia de lo que ocurre con el intervalo relativista ds² considerado dentro de la Teoría Especial de la Relatividad para un espacio-tiempo plano como el que nos retratan los diagramas espacio-tiempo de Minkowski, a ese mismo intervalo relativista ds² en la Teoría General de la Relatividad se le conoce ya sea con el nombre de métrica y con el nombre de elemento de línea, pero en realidad el concepto esencial sigue siendo el mismo extendido para un espacio-tiempo curvo.) La métrica que se acaba de dar arriba es la métrica que corresponde a una masa perfectamente esférica sin rotación alguna. Obsérvese con sumo cuidado que en esta métrica no estamos utilizando las coordenadas Cartesianas (x, y, z) que habíamos venido utilizando hasta ahora sino que estamos utilizando coordenadas esféricas. (r, θ, φ). En la Teoría General de la Relatividad podemos utilizar no sólo otros tipos de coordenadas sino inclusive podemos inventar nuestros propios sistemas de coordenadas como las coordenadas Kruskal-Szekeres inventadas por Martin Kruskal y George Szekeres (tomando como base la métrica de Schwarzchild) para describir el comportamiento del espacio-tiempo curvo en el interior del horizonte de uno de los objetos más interesantes cuya existencia es predicha por la Teoría General de la Relatividad: los agujeros negros.
Todo lo que sea invariante tiene un interés central en todo lo que tenga que ver con la Teoría de la Relatividad en virtud de un corolario de los postulados básicos conocido como el Principio de covariancia, el cual nos dice que las leyes de la física deben tomar la misma forma en todos los marcos de referencia. La covariancia de Lorentz (y análogamente la contravariancia de Lorentz) o principio especial de la relatividad se refiere a la propiedad de ciertas ecuaciones físicas de no cambiar de forma bajo cambios de coordenadas de un tipo particular. Las leyes de la física tienen que tomar la misma forma en todos los marcos de referencia inerciales. El requerimiento de covariancia de Lorentz afirma concretamente que si dos observadores usan coordenadas (x,y,z,ct) y (x',y',z',ct') tales que ambas se pueden relacionar mediantes las ecuaciones de transformación de Lorentz de las coordenadas, entonces cualesquiera dos ecuaciones que relacionen magnitudes que presentan covariancia de Lorentz se escribirán de la misma forma para ambos observadores. Por lo tanto una magnitud, ecuación o expresión matemática que presenta covariancia de Lorentz responderá a la mismas “leyes” o ecuaciones para todos los sistemas inerciales (es importante notar que si comparamos las medidas de un observador inercial con las de un observador no inercial que se está acelerando en vez de mantener su movimiento a una velocidad constante, la forma de las ecuaciones será diferente, lo cual se dá no sólo en la mecánica relativística sino en la mecánica Newtoniana en donde el estudio del movimiento de un cuerpo visto desde un sistema no-inercial en rotación requiere la inclusión de la fuerza centrífuga y la fuerza de Coriolis, y por tanto sus ecuaciones para explicar el movimiento de un móvil cuentan con términos adicionales a las que escribiría un observador inercial, y por tanto las ecuaciones de movimiento no tienen la misma forma para un observador inercial que para uno no inercial.)
Un ejemplo de la aplicación del principio de covariancia lo sería la ley del gas ideal:
PV = nRT
en donde P es la presión del gas contenido en un recipiente, V el volumen del gas dentro del recipiente, n es el número de moles del gas, R es la constante del gas ideal y T es la temperatura del gas. Esta es la fórmula que obtendría un observador en reposo en su laboratorio haciendo mediciones experimentales. Pero si el observador que está dentro de su laboratorio haciendo los experimentos para llegar a la anterior fórmula pasa a gran velocidad frente a nosotros en su marco de referencia S (o nosotros pasamos a gran velocidad frente a él), entonces dentro de nuestro marco de referencia S', haciendo mediciones sobre lo que él tiene en su laboratorio en su marco de referencia S nosotros debemos obtener la misma fórmula:
P’V’ = nRT’
ya que si no la obtuviéramos así, si la hubiéramos obtenido en otra forma, entonces habríamos encontrado una manera de medir el movimiento absoluto. Y si la fórmula cambia, entonces tenemos que encontrar la forma en la cual se pueda expresar dicha fórmula de modo tal que permanezca invariante.