Considerando para fines ilustrativos una velocidad de la luz de c = 1 metro por segundo, el diagrama espacio-tiempo para un rayo de luz es el siguiente:
Sobre el mismo diagrama, la especificación de la coordenada x de una partícula material que nos indica la posición en la cual se encuentra la partícula y del tiempo t al que corresponde esta coordenada, se dice que determina un evento o un suceso. Si representamos la posición x en el eje de las abcisas (eje horizontal) y el tiempo t en las ordenadas (eje vertical), cada punto del plano x-t corresponde a un posible evento. En un diagrama así podemos representar dos eventos distintos vistos por un mismo observador, trátese de dos eventos distintos que ocurren en el mismo lugar en tiempos diferentes, dos eventos distintos que ocurren al mismo tiempo en distintos lugares, o dos eventos distintos que ocurren en tiempos diferentes en lugares diferentes, como es el siguiente caso:
El lugar en un plano x-t de los eventos que representan las coordenadas apareadas de una partícula en varios instantes se conoce en los estudios de la relatividad como línea del mundo (world line) y también como línea del universo. En la Teoría Especial de la Relatividad, la línea del mundo es siempre una línea recta como la línea azul que tenemos en el diagrama de arriba porque la partícula material viaja siempre en movimiento rectilíneo en una misma dirección, recorriendo distancias iguales en tiempos iguales. Si en el instante t1 la coordenada de una partícula móvil es x1, entonces las magnitudes x1 y t1 determinan el evento E1. Análogamente, x2 y t2 determinan el evento E2. Los eventos para un mismo y único observador están separados en el espacio por una distancia Δx = x2 - x1 y en el tiempo por una distancia Δt = t2 - t1.
En los estudios sobre la relatividad, no se acostumbra revolver peras con manzanas, no se acostumbra revolver metros con segundos al medir sobre coordenadas rectangulares. Para que en un diagrama espacio-tiempo tanto el eje horizontal como el eje vertical usen el mismo tipo de unidades, se acostumbra multiplicar el tiempo en el eje vertical que corresponde al tiempo por la constante universal absoluta que es la velocidad de la luz c, ya que con ello ct se convierte en una distancia que está medida en metros, no en segundos. De este modo, no mezclamos peras con manzanas, al medir tanto en el eje vertical como en el eje horizontal lo estamos haciendo en metros. En todos los diagramas espacio-tiempo que serán utilizados aquí, la ordenada vertical estará en dimensiones de metros, o sea multiplicada por c, representado en la ordenada vertical como ct. Aunque aparezca t en lugar de ct, se sobreentenderá que siempre nos estamos refiriendo a ct. Además, para fines de simplificación, le seguiremos dando a c el valor de 1 metro por segundo. Sin embargo, para fines de cálculo numérico, estamos en libertad de regresar a las mediciones en segundos sobre el eje vertical.
En la última gráfica de arriba, tenemos representados dos eventos distintos, uno ocurriendo en la posición x1 en un tiempo representado en la posición ct1, y el otro evento ocurriendo en la posición x2 en un tiempo representado en la posición ct2. Poniendo números y usando una velocidad de la luz igual a c = 1 metro/segundo, las coordenadas respectivas de cada evento y la distancia entre ambos eventos es:
x1 = 1 metro
x2 = 2 metros
ct1 = 1 metro
ct2 = 3 metros
Δx = x2 - x1 = 2 metros - 1 metro = 1 metro
cΔt = ct2 - ct1 = 3 metros - 1 metro = 2 metros
x2 = 2 metros
ct1 = 1 metro
ct2 = 3 metros
Δx = x2 - x1 = 2 metros - 1 metro = 1 metro
cΔt = ct2 - ct1 = 3 metros - 1 metro = 2 metros
PROBLEMA: Una vara de medir de tres metros de largo se encuentra en reposo en el marco de referencia del observador O, y sus extremos coinciden con las coordenadas x1 = 2 metros y x2 = 5 metros. Trazar las líneas del mundo de los extremos de la vara de medir en un diagrama espacio-tiempo del observador O.
El diagrama espacio-tiempo pedido es el siguiente:
No es un requisito indispensable que en la construcción de un diagrama del espacio-tiempo se utilicen ejes ortogonales (perpendiculares, puestos en ángulos rectos el uno con respecto al otro). Es factible e inclusive deseable por razones que pronto serán obvias construír el diagrama espacio-tiempo utilizando ejes que no son perpendiculares. A continuación tenemos un diagrama en el cual los ejes principales no son perpendiculares:
Obsérvese la manera de leer las coordenadas de un punto cualesquiera en este tipo de diagrama, trazando desde el punto líneas paralelas a uno de los ejes principales hasta topar con el eje principal de la otra coordenada.
Y a continuación tenemos otro diagrama espacio-tiempo en el cual los ejes principales tampoco son perpendiculares:
Para un mismo observador, el anterior diagrama espacio-tiempo nos dá la distancia Δx que separa dos eventos E1 y E2, y nos dá también la distancia cΔt que separa a dichos eventos. Pero este diagrama espacio-tiempo describe la situación de un solo observador. El diagrama espacio-tiempo para un observador solitario no nos es de mucha utilidad en la resolución de problemas propios de la relatividad. Es necesario juntar de alguna manera los diagramas espacio-tiempo de dos observadores que están en movimiento relativo el uno con respecto al otro en uno solo. Lo que estamos buscando es algo que geométricamente nos permita visualizar en un mismo diagrama la situación de dos observadores. Esto se logra con un procedimiento que nos fue dado por el matemático Hermann Minkowski que será dado a continuación.
Procedimiento para construír un diagrama espacio-tiempo
(1) Supondremos que la velocidad de la luz tiene un valor de c = 1 metro/segundo. Empezamos trazando dos coordenadas perpendiculares que representan el diagrama espacio-tiempo de un observador al cual llamaremos O y que se considera a sí mismo en estado de reposo en su marco de referencia S, con la coordenada horizontal asignada a la representación de la posición de un objeto en el eje-x y con la coordenada vertical asignada a la representación del tiempo en el cual el objeto está en cierta posición:
(2) El diagrama espacio-tiempo más elemental que combina a dos observadores es el diagrama trivial en el cual ambos observadores está reposo el uno frente al otro en el mismo lugar (x = x’) y tienen sus relojes sincronizados al mismo tiempo (t = t’), lo que permite que los orígenes de ambos sistemas de referencia S y S’ coincidan en un mismo punto:
En forma similar a como sucede para el observador O, el eje ct’ es el lugar de los puntos tales que los eventos que ocurren a lo largo de dicho eje ocurren en el mismo lugar x’ = 0 pero en tiempos distintos para un observador O.
(3) Para trazar un diagrama espacio-tiempo combinado juntando a dos observadores diferentes que están en movimiento relativo el uno con respecto al otro a una velocidad V, trazamos primero el eje-t’ del marco de referencia S’ sobre el diagrama espacio-tiempo del observador en reposo usando para ello la velocidad relativa entre ambos observadores. No es necesario que los orígenes de los diagramas espacio-tiempo del observador O y del observador O’ coincidan, esto es mera cuestión de conveniencia. Construiremos un diagrama en el que ambos orígenes coinciden.
Suponiendo que la velocidad relativa entre ambos marcos de referencia es de V = 0.4c (o.4 metros/segundo) entonces para moverse una distancia x = 1 metro el observador O’ debe de haberse movido en un tiempo t = x/V = 2.5 segundos con respecto al origen, y para moverse una distancia x = 2 metros el observador O’ debe de haberse movido en un tiempo t = x/V = 5 segundos. Todos estos puntos están conectados con una línea recta, la cual trazamos sobre el diagrama como se muestra arriba. Esta recta corresponde al tiempo t’ del marco de referencia S’. Obsérvese que entre menor sea la velocidad relativa V más y más cercana estará la línea que hemos trazado a la vertical que corresponde a t, hasta que ambas llegan a coincidir cuando la velocidad relativa entre los dos observadores es cero. Para mayor simplicidad, prescindiremos de las graduaciones que hemos puesto en las coordenadas de ambos ejes del observador O:
(4) A continuación trazamos sobre el diagrama espacio-tiempo la ruta que corresponde a la trayectoria de un rayo de luz con una velocidad c = 1 metro/segundo:
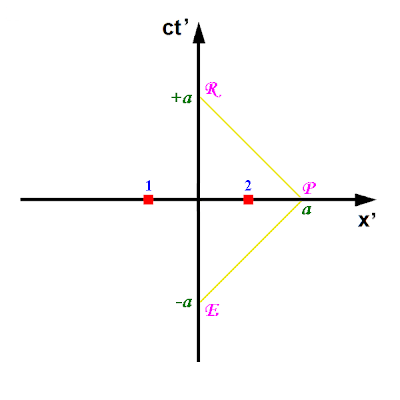
(5) Ahora vamos a trazar la coordenada de x’ superimponiéndola en el mismo diagrama. Para poder localizarla en dicho diagrama, considérese primero un rayo de luz lanzado en el marco de referencia del observador O’ en un tiempo (medido en metros) ct’ = -a desde la coordenada x’ = 0, un evento al que llamaremos E, el cual es reflejado en sentido opuesto en un tiempo ct = 0 por un espejo en un evento al que llamaremos P, para regresar nuevamente a la coordenada x’ = 0 en un evento al que llamaremos R ocurriendo en el tiempo ct’ = +a (podemos imaginar lo que ocurre como una descripción geométrica en el espacio-tiempo del experimento llevado a cabo por el viajero en el ferrocarril al que vimos en la entrada titulada “La física es parada de cabeza” cuando nos encontramos por vez primera el efecto relativista de la dilatación del tiempo):
Desde la perpectiva del observador estacionario O, la situación del rayo de luz que fue reflejado en el marco de referencia de O’ es la siguiente:
Tanto en el marco de referencia del observador O’ como en el marco de referencia del observador O la luz sigue teniendo la misma velocidad, como lo enuncia el segundo postulado de la Teoría Especial de la Relatividad. Por lo tanto, el rayo de luz que es lanzado en el marco de referencia de O’ también tendrá la misma pendiente de 45 grados en el marco de referencia de O. En el diagrama de arriba ubicamos arbitrariamente sobre el eje ct’ el evento E en el punto ct’ = -a, y trazamos desde dicho punto una trayectoria de 45 grados que corresponde al rayo de luz que es lanzado por el observador O’. Por otro lado, ubicamos sobre el eje t’ el evento R en el punto ct’ = +a, y trazamos desde allí la trayectoria que representa el rayo de luz reflejado por el espejo desde el punto que debe representar al evento P, una línea recta también de 45 grados (en concordancia con el segundo postulado de la Teoría Especial de la Relatividad) pero yendo de derecha a izquierda, extendiendo dicha línea hasta que se cruce con la otra línea que habíamos trazado. Esto nos dá unívocamente en el diagrama la localización del evento P. Por último, trazamos una línea punteada que conecta el origen común de ambos observadores hasta el punto que representa al evento P. Esta es la línea que corresponde a la coordenada de x’. No tardamos en descubrir que el ángulo que forma la coordenada x con la coordenada x’ es el mismo ángulo que el que forma la coordenada ct con la coordenada ct’. Con esto, hemos terminado esencialmente con la construcción del diagrama.
Una cosa que resalta del diagrama espacio-tiempo final es el hecho de que los dos eventos identificados con cuadritos rojos y con los números 1 y 2 que son simultáneos para el observador O’ (ambos ocurren en su tiempo t’ = 0) no ocurren al mismo tiempo en el marco de referencia del observador O. Esta es nuestra perspectiva geométrica del verdadero origen de los fenómenos relativistas de dilatación del tiempo y contracción de longitud: la simultaneidad deja de ser absoluta. En el universo de los absolutos, en la física pre-relativista, si dos eventos ocurrían al mismo tiempo para un observador estacionario, también ocurrían al mismo tiempo para otro observador en movimiento, lo cual deja de ser válido en la Teoría Especial de la Relatividad.
Una cosa que no hemos hecho y la cual dejaremos pendiente por el momento es graduar (marcar con divisiones igualmente espaciadas) las coordenadas (x,t) del observador O y las coordenadas (x’,t’) del observador O’ de modo tal que podamos resolver gráficamente un problema relativista obteniendo aproximaciones numéricas al igual que como lo hacen los ingenieros que utilizan papel gráfico para la resolución aproximada de problemas de otra índole (el Smith Chart utilizado para la resolución de problemas eléctricos de líneas de transmisión, y el diagrama de humedad o carta psicométrica usada para la resolución de problemas de humedad relativa y punto de rocío). Esta graduación es conocida también como la calibración de los ejes, y se puede llevar a cabo mediante cálculos numéricos con las ecuaciones de transformación de Lorentz que veremos posteriormente o con el procedimiento geométrico de la hipérbola invariante.
Así pues, nuestro principal medio de trabajo para el análisis geométrico de los problemas de la Teoría Especial de la Relatividad es el diagrama espacio-tiempo de Minkowski:
Este es el diagrama espacio-tiempo desde la perspectiva del observador O en reposo. Si queremos, podemos dibujar también el diagrama espacio-tiempo desde la perspectiva del observador O’ cuando este se considera en reposo y cuando ve al observador O en movimiento hacia la izquierda:
En esencia, lo que hemos hecho a sido tomar el diagrama básico para un observador O en reposo en un marco de referencia S, trazando sobre el mismo la línea que marca la trayectoria de un rayo de luz con una pendiente de 45 grados que corresponde a una velocidad c de 1 metro por segundo:
y sobre este diagrama, usando como referencia común la bisectriz que ambos diagramas deben tener identificando en el mismo la línea del mundo de un rayo de luz común a ambos observadores O y O’ en los marcos de referencia S y S’, hemos agregado al diagrama del observador estacionario O el siguiente diagrama espacio-tiempo de O’ (nos queda pendiente el asunto de cómo se lleva a cabo la graduación o calibración de los ejes x’-t’):
para así tener el siguiente diagrama espacio-tiempo combinando a ambos observadores desde la perspectiva del observador estacionario O:
PROBLEMA: Representar en un diagrama espacio-tiempo cuatro eventos distintos cuyas coordenadas son las siguientes:
E1(x1, c t1) = (1, 2)
E2(x2, c t2) = (2, 5)
E3(x’1, c t’1) = (4, 1)
E4(x’2, c t’2) = (2, 2)
E2(x2, c t2) = (2, 5)
E3(x’1, c t’1) = (4, 1)
E4(x’2, c t’2) = (2, 2)
Los eventos E1 y E2 están especificados sobre las coordenadas del observador en reposo O en su marco de referencia S, y en el diagrama espacio-tiempo combinado estarán ubicados en las siguientes posiciones (se han representado los dos eventos en el diagrama con unos cuadritos de color púrpura):
Los eventos E3 y E4 están especificados sobre las coordenadas del observador en movimiento O’ en su marco de referencia S’, y en el diagrama espacio-tiempo combinado estarán ubicados en las siguientes posiciones (se han representado los dos eventos en el diagrama con unos cuadritos de color verde):
Cuanto más alta sea la velocidad relativa V entre dos marcos de referencia acercándose o alejándose a una velocidad cada vez más cercana a la velocidad de la luz, tanto más se irán cerrando los ejes que corresponden al marco de referencia en movimiento S’ como podemos apreciarlo en el siguiente diagrama espacio-tiempo:
En el diagrama espacio-tiempo de arriba, tenemos sobrepuestos a tres observadores, el observador que consideramos estacionario, el observador O’ que se está moviendo a una velocidad relativa V con respecto al observador O, y un tercer observador O’’ que se está moviendo a una velocidad todavía mayor con respecto al observador O. Nótese cómo se van cerrando cada vez más y más los ejes coordenados x-t de un observador móvil conforme va aumentando su velocidad V con respecto al observador estacionario.
Cuando se prescinde de un diagrama espacio-tiempo como el caso en el que se vaya a efectuar un cálculo numérico, para la especificación completa de un mismo evento E cualquiera se deben especificar cuatro coordenadas, las coordenadas (x,t) del evento en el marco de referencia S, y las coordenadas (x’,t’) del evento en el marco de referencia S’, de modo tal que un evento quedará registrado como E(x,t,x’,t’) en forma completa. Esto es válido para cualquier evento. El único evento que tendrá las mismas coordenadas tanto para S como para S será el que ocurra en el punto común de origen, o sea E(x,t,x’,t’) = (0,0,0,0). En todos los demás casos las coordenadas diferirán. Sin embargo, al hablar de un evento se está hablando de un mismo y único evento visible para todos los observadores. Cuando un carro choca contra otro, ya sea visto por un observador estacionario o por un observador móvil, no existen dos marcos de referencia distintos en los cuales uno de los carros choque y el otro no. Distintos observadores siempre se podrán poner de acuerdo en un evento específico, cada uno asignándole sus propias coordenadas. En lo que no se podrán poner de acuerdo es en la duración del lapso de tiempo entre dos eventos distintos E1 y E2 y en la distancia espacial que separe a dos eventos distintos. Un observador dirá que el lapso de tiempo entre dos eventos E1 y E2 fue Δt mientras que el otro dirá que fue Δt’. Un observador dirá que la distancia espacial entre dos eventos fue Δx mientras que el otro dirá que fue Δx’, y en los diagramas de arriba podemos ver por qué no podrán ponerse de acuerdo jamás, a menos de que tomen en cuenta las correciones relativistas.
Dado un evento E cualquiera puesto en un diagrama espacio-tiempo que involucre a dos observadores en movimiento relativo el uno con respecto al otro, las coordenadas del mismo se pueden obtener tanto en un marco de referencia como en el otro trazando desde el evento líneas paralelas a cada uno de los ejes coordenados respectivos de cada observador, como lo muestra el siguiente diagrama:
En el diagrama espacio-tiempo de arriba tenemos un evento A. Trazando una línea horizontal hacia la izquierda hasta llegar al eje vertical ct podemos obtener el valor de ct con lo cual podemos obtener el tiempo, y trazando una línea vertical hacia abajo podemos obtener la coordenada de la distancia x. Del mismo evento A podemos hacia la línea ct’ una línea paralela a la coordenada x’ con lo cual obtenemos el valor de ct’, y podemos trazar hacia abajo otra línea paralela a ct con lo cual obtenemos el valor de x’.
PROBLEMA: Mediante un diagrama espacio-tiempo, obtener y explicar el efecto relativista de la dilatación del tiempo.
El análisis se llevará a cabo considerando a nuestro proverbial viajero el cual dentro de un vagón de ferrocarril arroja un rayo de luz hacia arriba desde una linterna, el cual es reflejado por un espejo regresando al punto de partida, mientras que un observador sentado a un lado de las vías del ferrocarril observa al rayo de luz recorrer una trayectoria mayor. En la construcción de cualquier diagrama espacio-tiempo se vuelve necesario identificar claramente los eventos que ocurren. En este caso, nos basta con identificar sobre el diagrama espacio-tiempo dos eventos: el primer evento que llamaremos E1 ocurre cuando el rayo de luz sale de la linterna, y el segundo evento que llamaremos E2 ocurre cuando el rayo de luz regresa reflejado por el espejo al punto desde donde fue lanzado. Ambos eventos ocurren en el mismo lugar para el observador viajero O’, al cual le asignaremos la coordenada x’ = 0, pero en tiempos diferentes t’1 y t’2. Una vez localizados ambos eventos en el sistema de referencia S’ de O’, nos basta con trazar dos líneas horizontales desde las coordenadas (x’, t’1) y (x’, t’2) hacia el eje de tiempos del observador O para obtener las coordenadas correspondientes en el marco de referencia de O de los dos eventos:
Darse cuenta de que efectivamente hay una dilatación del tiempo requiere que pongamos sobre los ejes del diagrama espacio-tiempo divisiones graduadas en los ejes de los tiempos, o sea que llevemos a cabo la calibración de los ejes, lo cual se verá en una entrada posterior. Obsérvese que a diferencia de como sucede con el observador O’, los eventos E1 y E2 no sólo ocurren en tiempos diferentes t1 y t2; también ocurren en lugares diferentes x1 y x2.
PROBLEMA: Ilustrar mediante un diagrama espacio-tiempo el fenómeno de la contracción de longitud sobre una vara de medición, suponiendo que:
a) El observador en reposo O es el que tiene la vara de medir y el observador O’ es el que la ve pasar frente a él.
b) El observador en movimiento O’ es el que lleva consigo la vara de medir y el observador en reposo O es el que la ve pasar frente a él.
a) En el primer caso, si el observador en reposo es el que tiene una vara de medir de longitud L0, las líneas del mundo de los dos extremos de la vara de medir se mantendrán como dos líneas verticales paralelas proyectadas hacia arriba como lo muestra el siguiente diagrama espacio-tiempo:
En este caso, el observador estacionario O mide para la vara al mismo tiempo t = 0 en su tiempo propio una longitud L0. Pero el observador móvil O’ mide la coordenada de cada extremo de la vara en tiempos diferentes y concluye que hubo una contracción en la longitud de la vara.
b) En el segundo caso, si el observador en movimiento O’ es el que lleva consigo la vara de medir de longitud L0, las líneas del mundo de los dos extremos de su vara de medir se mantendrán como dos líneas paralelas las cuales a su vez serán paralelas a su eje vertical ct’ como lo muestra el siguiente diagrama espacio-tiempo:
En este caso, el observador O’ mide para su vara al mismo tiempo t’ = 0 en su tiempo propio una longitud L0. Pero el observador O mide la coordenada de cada extremo de la vara en tiempos diferentes y concluye por su parte que hubo una contracción en la longitud de la vara.
Hemos visto una forma convencional del diagrama espacio-tiempo de Minkowski, pero no es la única manera de construír un diagrama espacio-tiempo. Otra forma de lograrlo es recurriendo a un truco. El truco consiste en que sobre un mismo diagrama, usando el mismo origen para dos observadores distintos que se están moviendo a una velocidad relativa V el uno con respecto al otro, se tracen dos ejes de espacios correspondiendo a los espacios propios medidos por cada observador, y además se tracen dos ejes de tiempos correspondiendo a los tiempos propios medidos por cada observador, de modo tal que el eje de tiempos de un observador sea perpendicular al eje de espacios del otro observador y que el eje de espacios de dicho observador sea perpendicular al eje de espacios del otro observador. Esto es lo que nos produce esencialmente lo que se llama un diagrama espacio-tiempo de Loedel, así llamado en referencia a su creador, el físico latinoamericano Enrique Loedel Palumbo:
El diagrama de Loedel es una modificación con fines didácticos del diagrama espacio-tiempo que fue concebido por Hermann Minkowski.
Ahora veremos con mayor detalle el asunto de la simultaneidad, visto desde la óptica de la Teoría Especial de la Relatividad.
El primer contacto que tienen muchos estudiantes con la explicación de la pérdida de la simultaneidad absoluta se basa en un ejemplo como el siguiente en el cual tenemos a nuestro proverbial pasajero de ferrocarril colocado justo a la mitad de los dos extremos del convoy de vagones. En el marco de referencia S del observador situado a un lado de las vías del ferrocarril justo a la mitad de dos torres de luz se activan en forma sincronizada (al mismo tiempo) dos pulsos luminosos emanados de las dos torres de luz usando relojes sincronizados en el marco de referencia de S para lanzar los pulsos luminosos, en forma tal que el estallido de uno de los pulsos luminosos coincidirá justo con el extremo delantero del ferrocarril y el estallido del otro pulso luminoso coincidirá justo con el extremo trasero del ferrocarril:
El observador estático situado a un lado de las vías del ferrocarril en el marco de referencia S recibe los dos pulsos luminosos al mismo tiempo, y por lo tanto concluye que ambos eventos fueron simultáneos dentro de su marco de referencia. Por su parte, en virtud de que la luz tiene una velocidad finita y en virtud de que el pasajero del ferrocarril está en movimiento rápido, uno de los pulsos luminosos le llega primero que el otro, y el pasajero concluye que los destellos no ocurrieron al mismo tiempo, que no fueron simultáneos, dada la diferencia de tiempos en que tardan en llegarle los dos rayos de luz a su plataforma móvil, y por lo tanto para él los eventos no son simultáneos en su marco de referencia S’.
La anterior es una explicación simplista y en cierta forma errónea porque no toma en cuenta para nada los efectos relativistas de la dilatación del tiempo y la contracción de longitud. La pérdida en la simultaneidad se debe, según la explicación anterior, a la velocidad finita de la luz. Si no hubiese dilatación del tiempo ni contracción de longitud, si no hubiese relatividad, si existiesen el tiempo absoluto y el espacio absoluto, la pérdida en la simultaneidad sería meramente una ilusión, una pérdida de simultaneidad aparente. La situación actual es más complicada que la descrita en el ejemplo anterior precisamente porque hay efectos relativistas de dilatación del tiempo y contracción de longitud. Efectivamente, hay una diferencia de tiempos en la llegada de los dos pulsos luminosos al viajero en el ferrocarril, pero también hay una pérdida de simultaneidad real que no es ocasionada por la velocidad finita de la luz sino por efectos de índole relativista, y es en este caso en donde los diagramas espacio-tiempo de Minkowski resultan de una ayuda invaluable para entender lo que está sucediendo, permitiéndonos ir más allá de la anterior explicación simplista. Para entender lo que está sucediendo, es necesario identificar a los dos eventos que ocurren simultáneamente en el marco de referencia S como E1 y E2 y ver las coordenadas (x’,t’) de cada uno de dichos eventos en el marco de referencia S’.
Si dos eventos ocurren al mismo tiempo en el mismo lugar se puede afirmar sin lugar a dudas que ambos eventos son simultáneos. Cuando dos aviones chocan en el aire, no existe marco de referencia alguno en el cual la colisión de ambos aviones no sea simultánea. Pero entre mayor sea la distancia entre dos eventos que ocurren en distintos lugares tanto mayor será la dificultad para los observadores en decidir por cuenta propia el asunto de la simultaneidad.
Considérese el siguiente diagrama espacio-tiempo de Minkowski que ilustra la situación de eventos que son simultáneos en un marco de referencia S del observador O y que NO son simultáneos en un marco de referencia S’ del observador O’, así como eventos que son simultáneos en un marco de referencia S’ pero que NO son simultáneos en el marco de referencia S:
En este diagrama, los eventos A y B ocurren simultáneamente a un mismo tiempo en el marco de referencia S en dos lugares distintos que podemos identificar como x1 y x2. Pero resulta claro que, relativísticamente hablando, los mismos eventos A y B ocurren en tiempos diferentes en el marco de referencia de S’, los cuales podemos ubicar en los tiempos t’1 y t’2. Los dos eventos A y B ocurren en tiempos diferentes en lugares diferentes para un observador situado en S’. Aquí lo que es simultáneo para S no es simultáneo para S’. Por otro lado, los eventos C y D ocurren simultáneamente a un mismo tiempo en el marco de referencia S’ en dos lugares distintos que podemos identificar como x’3 y x’4. Pero resulta claro que, relativísticamente hablando, los mismos eventos C y D ocurren en tiempos diferentes en el marco de referencia de S, los cuales podemos ubicar en los tiempos t3 y t4. Los dos eventos C y D ocurren en tiempos diferentes en lugares diferentes para un observador situado en S. Aquí lo que es simultáneo para S’ no es simultáneo para S. Y en cuanto a los eventos E y F, tales eventos no son simultáneos ni para S ni para S’. Todo esto lo podemos ver claramente tal como es en los diagramas espacio-tiempo de Minkowski. Desafortunadamente, aunque estos gráficos son de gran ayuda, no se prestan para cálculos numéricos de precisión, para lo cual tendremos que recurrir a una herramienta algebraica conocida como las ecuaciones de transformación de Lorentz.
A continuación tenemos otro diagrama espacio-tiempo que nos ilustrara la falla de la simultaneidad dentro de la Teoría Especial de la Relatividad:
En este diagrama espacio-tiempo, para el observador en el marco de referencia S cuyas coordenadas son (x, ct), dos eventos son simultáneos cuando de acuerdo con su reloj ocurren al mismo tiempo t = t0 en dos lugares diferentes que podemos identificar simplemente como x1 y x2, marcados por los puntos obscuros que están puestos sobre la línea horizontal que corresponde a un tiempo t = t0.
Sin embargo, para el otro observador cuyas coordenadas son (x’, ct’), los dos eventos no ocurren simultáneamente, ocurre primero uno y después ocurre el otro. En su reloj un evento ocurre primero en el tiempo t’1 y el otro evento ocurre después en el tiempo t’2. Esta anomalía relativista en la simultaneidad es precisamente la que ocasiona los efectos físicos de la dilatación del tiempo y la contracción de longitud. Todas las dificultades para comprender las aparentes paradojas que están detrás de la Teoría Especial de la Relatividad surgen de nuestra renuencia a rechazar de manera definitiva el falso concepto de la simultaneidad absoluta. Si hubiera simultaneidad absoluta, no habría dilatación relativista del tiempo ni contracción de longitud, aunque ello requeriría neceariamente la aceptación del movimiento absoluto, lo cual a estas alturas ya hemos descartado por completo.
PROBLEMA: Mediante un diagrama espacio-tiempo, obtener y explicar el efecto relativista de la contracción de longitud.
Si en lugar de un diagrama espacio-tiempo trazado sobre una hoja hacemos un esfuerzo extra por representar dos coordenadas de la posición (x,y) y la coordenada del tiempo (ct) apuntando esta última hacia arriba, podemos dibujar algo que se conoce como superficies de simultaneidad tanto para el observador O en reposo en el marco de referencia S como el observador en movimiento O’ en el marco de referencia S’:
En el diagrama de la izquierda, tenemos dos eventos representados con puntitos rojos que ocurren al mismo tiempo, simultáneamente, en el marco de referencia S del observador O, y tenemos otros dos eventos representados con puntitos amarillos que ocurren en tiempos diferentes en el marco de referencia S’ del observador O’. Pero en el diagrama de la izquierda, los dos eventos representados con puntitos amarillos sí ocurren al mismo tiempo, simultáneamente, en el marco de referencia S’ del observador O’, aunque los eventos representados con puntitos rojos y que eran simultáneos en el marco de referencia S del observador O han dejado de ser simultáneos para el observador O’.
La limitante de que ningún objeto puede viajar a una velocidad mayor que la velocidad de la luz se refleja no tan sólo en un cuadrante del diagrama espacio-tiempo, se refleja en los cuatro cuadrantes, y el “origen” del observador puede no necesariamente coincidir con el origen del diagrama espacio-tiempo que está situado en x = 0 y ct = 0, en virtud de que la fijación de las coordenadas es una mera cuestión de conveniencia:
En el diagrama de arriba, tenemos a un cuerpo que al moverse del punto A al punto B se ha movido en línea recta de x1 = 0.5 metros y x2 = 0.75 metros a partir de un tiempo t1 = 0.5 segundos a un tiempo t1 = 1.75 segundos, siendo por lo tanto su velocidad igual a v = 0.2 c. Puesto que el avance natural del tiempo es siempre hacia arriba, el cuerpo sólo puede desplazarse también junto con el tiempo de abajo hacia arriba, en cualquier trayectoria rectilínea cuya pendiente no exceda la velocidad de la luz, lo cual está marcado por el área punteada. Del punto B hay un conjunto de puntos que marcan el futuro de la posición del cuerpo en el diagrama espacio-tiempo, y hay también un conjunto de puntos que marcan el pasado de la posición del cuerpo en el diagrama espacio-tiempo.
No es necesario limitarnos a un diagrama espacio-tiempo de tan sólo dos dimensiones. Podemos agregar una dimensión adicional, como correspondería a la coordenada y en un plano Cartesiano x-y, para tener lo que parece ser un cono dentro del cual están circunscritas las trayectorias posibles de un objeto, llamado cono de luz:
De este modo, podemos tener las siguientes dos trayectorias rectilíneas posibles en el siguiente diagrama espacio-tiempo tridimensional:
Antes del advenimiento de la Teoría Especial de la Relatividad, podíamos hablar acerca de un “ahora” universal, podíamos hablar acerca de un “pasado” común universal y acerca de un “futuro” común universal, comunes a todos los que habitamos en este Universo, puesto que el tiempo absoluto marchaba al unísono por igual en todo el Universo, sin retrasarse ni adelantarse en ninguno de sus confines:
Pero a partir del advenimiento de la Teoría Especial de la Relatividad, para cada observador hay un “pasado”, un presente y un “futuro”, delimitados por el cono de luz:
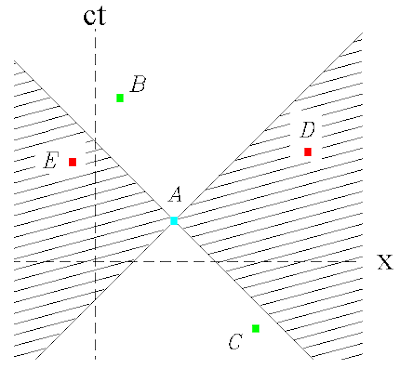
En este último diagrama, la línea del mundo (de color verde) corresponde a un observador que está en reposo. El punto en el que se tocan los dos conos de luz que corresponden al “pasado” y al “futuro” del observador viene siendo el “ahora” del observador. Puesto que ningún objeto puede moverse a una velocidad mayor que la velocidad de la luz, la única forma de poder llegar al “ahora” desde el pasado (suponiendo una línea del mundo con un movimiento rectilíneo) es haciéndolo dentro del cono de luz inferior. Y la única forma de poder llegar a cierto punto del diagrama espacio-tiempo en el “futuro” es estando dentro del cono de luz superior. Las regiones de espacio-tiempo de color gris en el diagrama de arriba son, por lo tanto, regiones de espacio-tiempo a las que el observador no tiene acceso. Esto fija de manera unívoca todas las relaciones que pueda haber de causa-efecto entre dos observadores. Los únicos eventos que pueden cambiar el estado de un observador o de un objeto en su posición actual en el espacio-tiempo deben estar situados en ó dentro del cono de luz que corresponde a su “pasado”. Y los únicos eventos que pueden ser influenciados por eventos en los que participe un observador o un objeto deben estar situados en ó dentro del cono de luz que corresponde a su “futuro”. De este modo, en el siguiente diagrama espacio-tiempo:
el evento que tuvo lugar en el punto C pudo muy bien haber cambiado lo que está sucediendo en el “ahora” del observador que se encuentra en el punto A, y el observador A puede hacer algo para intervenir sobre lo que sucede en el evento que tiene lugar en el punto B. Pero no puede hacer nada para modificar lo que ocurra en los eventos E y D porque están fuera de su alcance al no poder establecer una comunicación con ellos debido a la limitante absoluta de la velodidad de la luz. Los puntos E y D están en regiones prohibidas. Cabe aclarar que la línea en el diagrama que corresponde a la coordenada X no está inclinada como parece estarlo; es una línea perfectamente horizontal como puede comprobarlo el lector en el monitor de su computadora con la ayuda de una hoja de papel. Se trata de una ilusión óptica, como lo es la ilusión del concepto de la simultaneidad absoluta que tanto trabajo le cuesta a muchos estudiantes sepultar.
¿Entonces ya no podemos hablar de un pasado común y un futuro común a todos los habitantes del Universo como se acostumbraba hacerlo antes? Sí, pero desde la perspectiva relativista. En el siguiente diagrama espacio-tiempo tenemos los conos de luz que corresponden no a uno sino a dos eventos A y B:
En este diagrama, el “ahora” del evento A no puede tener efecto alguno sobre el “ahora” del evento B porque ello requeriría atravesar la zona gris que le está vedada a ambos eventos. Para poder tener efecto alguno sobre el “ahora” de B, el “ahora” del evento A debería ser capaz de poder transmitir información al “ahora” del evento B a una velocidad mayor que la velocidad de la luz, lo cual es imposible. Sin embargo, ambos conos de luz tienen dos zonas en común, las zonas en las cuales se traslapan los dos conos de luz. La zona común en la cual se traslapan los pasados de ambos, de color rosa, es la zona en la cual ambos eventos pueden intercambiar información que sea capaz de cambiar el “ahora” de cada uno de ellos, es la zona denominada pasado común. Y la zona común en la cual se traslapan los futuros de ambos, de color azul cielo, es la zona en la cual ambos eventos podrán intercambiar información en su futuro (a menos de que ocurra un cambio en la línea del mundo de uno de ellos o de ambos), es la zona denominada futuro común. De cualquier manera, y hablando del Universo como un todo, sí podemos hablar de un “ahora” universal que sin embargo no es un “ahora” absoluto, porque en la infinitud de las regiones locales de las que está hecho el Universo habrá variaciones en la marcha del tiempo como las que predice la Teoría de la Relatividad.
En los diagramas espacio-tiempo que hemos visto, sólo hemos considerado objetos que mantienen una trayectoria rectilínea a velocidad constante sobre la cual se pueden aplicar los principios propios de la Teoría Especial de la Relatividad. Pero también podemos trazar en un diagrama espacio-tiempo la trayectoria de un objeto que no mantiene una trayectoria rectilínea, que está cambiando constantemente de dirección. Un diagrama tal tendría un aspecto como el siguiente:
En esta trayectoria tenemos a un viajero que se ha trasladado del punto P al punto Q en un lapso de tiempo Δτ medido en el reloj con el que va viajando el viajero. Este es precisamente el tipo de movimientos que deben caer bajo el ámbito de una teoría expandida para analizar movimientos no-rectilíneos o acelerados, una Teoría General de la Relatividad. La trayectoria de un cuerpo que no avanza en línea recta dentro del cono de luz debe ser tal que la velocidad de la luz nunca debe ser excedida, o sea que la tangente de la curva nunca debe apartarse más de 45 grados del eje vertical que representa a la coordenada del tiempo. A continuación tenemos un ejemplo de un recorrido válido y un recorrido inválido:
Obsérvese del diagrama anterior izquierdo cómo el cono de luz es algo que viaja junto con el observador móvil, el cual puede definir en cualquier momento cuál será el instante en que su reloj sea ajustado para marcar el “pasado”, el “futuro” y el “presente” (el instante a partir del cual se empieza a tomar el tiempo para llevar las cuentas de una sucesión de eventos).
Partiendo de sus dos postulados, Einstein dedujo correctamente las nuevas leyes para las transformaciones llevadas a cabo entre dos marcos de referencia distintos, formalizadas algebraicamente con las ecuaciones de transformación de Lorentz, pero fue Hermann Minkowski el que demostró que si dejábamos de ver a las tres dimensiones del espacio y a la dimensión del tiempo como entidades separadas y las uníamos geométricamente en un espacio-tiempo de cuatro dimensiones, entonces las transformaciones relativistas podían ser vistas como correspondiendo a rotaciones llevadas a cabo en este espacio-tiempo cuatri-dimensional, lo cual fue una enorme simplificación creando una nueva perspectiva acerca del espacio y del tiempo. Al principio Einstein no dió mucha importancia a la interpretación geométrica de Minkowski, tomándola meramente como una formalidad matemática sin significado físico real, pero eventualmente cambió su actitud adoptando el punto de vista cuatri-dimensional geométrico que después emplearía para la postulación de la Teoría General de la Relatividad.