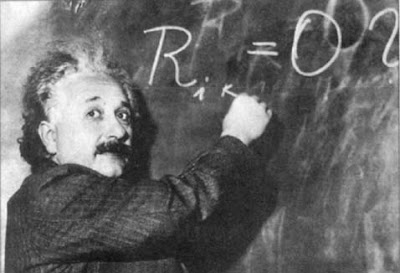curvatura geométrica = densidad de masa-energía
y si este concepto será enunciado de modo tal que será independiente del sistema de coordenadas empleado para describirlo, entonces habiendo estado expuestos al tensor de curvatura de Riemann nuestra primera ocurrencia tal vez será emplearlo directamente en una igualdad tensorial como la siguiente:
R = kT
en donde k es una simple constante de proporcionalidad (como 8π). El problema con este primer intento es que siendo el tensor de Riemann un tensor de orden cuatro la igualdad tensorial requeriría que el tensor energía-tensión T fuera también de orden cuatro. Pero ya vimos que para nuestros propósitos un tensor energía-tensión T de orden dos parece ser suficiente. Entonces, más que “estirar” a T convirtiéndolo en un tensor de orden cuatro, optaremos por convertir al tensor de curvatura de Riemann en otro tensor de curvatura de orden dos derivado de R, siempre y cuando no estemos sacrificando algo importante. Y lo primero que se nos viene a la mente es llevar a cabo una contracción tensorial del tensor de Riemann igualando dos de sus índices, lo cual lo convierte en un tensor de orden dos. Esto es precisamente lo que se logra con el tensor de Ricci. El tensor de Ricci es un tensor que se obtiene directamente del tensor de Riemann por una contracción de dos de sus índices. La elección del índice covariante a contraer no es fija (se aprovecha aquí la ocasión para recordar que el proceso de contracción activa automáticamente la convención de sumación para índices repetidos). La contracción se lleva a cabo entre el índice superior y el segundo índice inferior del tensor de Riemann.
Al llevar a cabo una contracción del tensor de Riemann, perdemos dos de los cuatro índices que especifican a los componentes de dicho tensor de curvatura. ¿Por qué razón es suficiente un tensor de dos índices para describir el efecto -sobre el movimiento de los cuerpos- de la curvatura causada en el 4-espacio de la Relatividad General por la presencia de masa-energía? Porque para describir una 2-superficie en un espacio N-dimensional basta con especificar dos coordenadas curvilíneas, y las trayectorias geodésicas de los cuerpos en movimiento se llevan a cabo precisamente sobre una 2-superficie (como ocurre con un satélite artificial que le está dando vueltas a la Tierra siguiendo la geodésica de un arco sobre una superficie esférica o elíptica imaginaria).
Partiendo de la definición del tensor de Riemann, el cual es un tensor de orden cuatro, contravariante de orden uno y covariante de orden 3:
Rαβμν = Γαβν,μ - Γαβμ,ν + Γασμ · Γσβν - Γασν · Γσβμ
si llevamos a cabo una contracción del primer índice y el tercer índice (el índice superior y el segundo índice inferior), obtenemos el siguiente tensor covariante de orden dos:
Rμβμν = R1β1ν + R2β2ν + R3β3ν + R4β4ν = Rβν
que está definido precisamente como el tensor de Ricci.
En principio, otras contracciones del tensor de Riemannn son posibles. Podemos llevar a cabo una contracción entre el primer índice y segundo índice (el índice superior y el primer índice inferior) y el primer índice y el cuatro índice (el índice superior y el tercer índice inferior), pero en virtud de que el tensor Rαβμν es antisimétrico en los índices α y β y en los índices μ y ν, todas estas contracciones terminan desvaneciéndose idénticamente o reduciéndose a Rβν ó -Rβν . En pocas palabras: El tensor de Ricci es la única contracción posible del tensor de Riemann.
PROBLEMA: A partir de la definición del tensor de Riemann, demuéstrese que el tensor de Ricci es la única contracción posible del mismo.
Empezaremos con el tensor de Riemann:
Rαβμν = ½ (gαν,βμ - gαμ,βν + gβμ,αν - gβν,αμ)
al cual le subiremos el primer índice con la ayuda del tensor métrico g con la finalidad de poder llevar a cabo una contracción con cada uno de los tres índices covariantes:
Rαβμν = gαxRxβμν
Rαβμν = gα1R1βμν + gα2R2βμν + gα3R3βμν + ...
Rαβμν = gα1R1βμν + gα2R2βμν + gα3R3βμν + ...
Llevaremos a cabo primero la contracción entre el índice superior α y el índice inferior β igualando ambos índices sobre la expresión anterior:
Rααμν = Rμν = gα1R1αμν + gα2R2αμν + gα3R3αμν + ...
El siguiente paso consiste en llevar a cabo la sumación sobre el índice contraído α. La expansión se llevará a cabo agrupando los sumandos de una manera cuya razón pronto será obvia:
Rμν =______________________
g11R11μν + g12R21μν + g13R31μν + ...
+ g21R12μν + g22R22μν + g23R32μν + ...
+ g31R13μν + g32R23μν + g33R33μν + ...
g11R11μν + g12R21μν + g13R31μν + ...
+ g21R12μν + g22R22μν + g23R32μν + ...
+ g31R13μν + g32R23μν + g33R33μν + ...
A continuación apelamos a la propiedad de hemi-simetría del tensor de Riemann demostrada previamente en una entrada correspondiente al tensor de Riemann, bajo la cual si intercambiamos los primeros dos índices el signo del componente se invierte:
Rαβμν = - Rβαμν
con lo cual obtenemos lo siguiente:
Rμν =______________________
g11R11μν + g12R21μν + g13R31μν + ...
- g21R21μν + g22R22μν + g23R32μν + ...
- g31R31μν - g32R32μν + g33R33μν + ...
g11R11μν + g12R21μν + g13R31μν + ...
- g21R21μν + g22R22μν + g23R32μν + ...
- g31R31μν - g32R32μν + g33R33μν + ...
Puesto que el tensor métrico g, por su propia definición, es un tensor métrico, gij = gji, entonces podemos introducir este hecho en lo anterior con lo que tras ello podemos proceder a la borradura de los términos positivos que son cancelados por los términos negativos:
Rμν =______________________
g11R11μν + g12R21μν + g13R31μν + ...
- g12R21μν + g22R22μν + g23R32μν + ...
- g13R31μν - g23R32μν + g33R33μν + ...
g11R11μν + g12R21μν + g13R31μν + ...
- g12R21μν + g22R22μν + g23R32μν + ...
- g13R31μν - g23R32μν + g33R33μν + ...
Esto nos deja únicamente con los siguientes términos “diagonales” en nuestro acomodo de términos :
Rμν = g11R11μν + g22R22μν + g33R33μν + ...
Sin embargo, cada uno de estos términos se va cancelando en virtud de la identidad que nos dice que en un tensor de Riemann cuando los primeros dos índices son iguales el valor se vuelve cero, o sea:
Rααμν = 0
Descartamos pues la primera posibilidad, la contracción entre el índice superior α y el índice inferior β, en virtud de que no nos dá ningún resultado útil más que el valor de cero.
Llevaremos a cabo ahora la contracción entre el índice superior α y el índice inferior μ igualando ambos índices sobre la expresión dada atrás anteriormente:
Rαβαν = Rβν = gα1R1βαν + gα2R2βαν + gα3R3βαν + ...
Procediendo como lo hicimos anteriormente, llevamos a cabo la expansión sobre la segunda contracción:
Rβν =______________________
g11R1β1ν + g12R2β1ν + g13R3β1ν + ...
+ g21R1β2ν + g22R2β2ν + g23R3β2ν + ...
+ g31R1β3ν + g32R2β3μν + g33R3β3ν + ...
g11R1β1ν + g12R2β1ν + g13R3β1ν + ...
+ g21R1β2ν + g22R2β2ν + g23R3β2ν + ...
+ g31R1β3ν + g32R2β3μν + g33R3β3ν + ...
Reagrupando y usando la propiedad de simetría del tensor métrico gij = gji, podemos llevar a cabo la siguiente simplificación:
Rβν =______________________
g11R1β1ν + g22R2β2ν + g33R3β3ν + ...
+ g21(R2β1ν + R1β2ν) + g13(R3β1ν + R1β3ν)
+ g23(R3β2ν + R2β3μν) + ...
g11R1β1ν + g22R2β2ν + g33R3β3ν + ...
+ g21(R2β1ν + R1β2ν) + g13(R3β1ν + R1β3ν)
+ g23(R3β2ν + R2β3μν) + ...
Este definitivamente no es un tensor cero, a menos de que todas las componentes del tensor de Riemann o todas las componentes del tensor métrico sean iguales a cero. Este es el tensor de Ricci.
Por último, llevaremos a cabo la tercera contracción posible que podemos llevar a cabo en el tensor de Riemann, la que se puede efectuar entre el índice superior α y el índice inferior ν igualando ambos índices sobre la expresión dada anteriormente:
Rαβμα = Rβμ = gα1R1βμα + gα2R2βμα + gα3R3βμα + ...
Procediendo como lo hicimos anteriormente, efectuamos la expansión de la contracción sobre el tercer índice:
Rβμ =______________________
g11R1βμ1 + g12R2βμ1 + g13R3βμ1 + ...
+ g21R1βμ2 + g22R2βμ2 + g23R3βμ2 + ...
+ g31R1βμ3 + g32R2βμ3 + g33R3βμ3 + ...
g11R1βμ1 + g12R2βμ1 + g13R3βμ1 + ...
+ g21R1βμ2 + g22R2βμ2 + g23R3βμ2 + ...
+ g31R1βμ3 + g32R2βμ3 + g33R3βμ3 + ...
Usando la propiedad del tensor de Riemann según la cual si intercambiamos los últimos dos índices el signo del componente se invierte:
Rαβμν = - Rαβνμ
y renombrando del lado derecho de la igualdad el índice μ como ν, obtenemos lo siguiente:
Rβμ =______________________
- g11R1β1ν - g12R2β1ν - g13R3β1ν - ...
- g21R1β2ν - g22R2β2ν - g23R3β2ν - ...
- g31R1β3ν - g32R2β3ν - g33R3β3ν - ...
- g11R1β1ν - g12R2β1ν - g13R3β1ν - ...
- g21R1β2ν - g22R2β2ν - g23R3β2ν - ...
- g31R1β3ν - g32R2β3ν - g33R3β3ν - ...
Pero esto último es esencialmente lo mismo que ya obtuvimos con anterioridad en un paso intermedio que nos conducía al tensor de Ricci, pero con el signo opuesto, o sea:
Rβμ = - Rβν
Esto no nos dá información nueva que no hubiéramos obtenido ya anteriormente. Así pues, de todas las contracciones que podemos llevar a cabo sobre el tensor de Riemann, escrito como Rαβμν, sólo obtenemos una contracción no trivial, precisamente el tensor de Ricci.
El tensor de Ricci era el tensor favorito de Einstein, esto en virtud de que la definición del tensor G de Einstein para formalizar matemáticamente la curvatura en el espacio-tiempo que se nos manifiesta como la gravedad depende directamente del tensor de Ricci. Él fue el primero en darse cuenta de la importancia de ese tensor para la construcción de una teoría de la gravedad. Encontrar soluciones a la ecuación fundamental de la Relatividad General equivale a buscar el tensor de Ricci que está asociado con la solución.
En la siguiente fotografía tenemos a Einstein en una visita famosa que hizo a Mount Wilson para agradecerle personalmente a Edwin Hubble su descubrimiento astronómico que permitió abandonar el modelo del Universo estático por un Universo inflacionario en expansión:
En esta fotografía Einstein escribió en el pizarrón lo siguiente:
Rik = 0 ?
El signo de interrogación que puso Einstein a la derecha de la expresión indica las dudas personales que ya albergaba sobre el modelo del Universo estático al cual se había aferrado y por el cual introdujo en su ecuación tensorial la constante cosmológica que tiempo después llamaría el error (intelectual) más grande de su vida.
Al presentar al mundo sus ecuaciones de campo, Einstein hizo la suposición central de que en el espacio vacío el tensor de Ricci tiene un valor de cero:
Rμν = 0
Esta expresión constituye esencialmente la ley de gravitación universal de Einstein. La frase “espacio vacío” significa aquí que no hay ningún tipo de materia presente (como un gas de polvo interestelar o partículas atómicas libres) ni hay campos físicos de ninguna índole excepto el campo gravitacional, el cual en sí no perturba este vacío a diferencia de otros campos (como el campo electromagnético) que sí lo hacen. Las condiciones de un espacio vacío se cumplen razonablemente bien para el espacio entre los planetas del sistema solar. El espacio-tiempo plano obviamente satisface la ecuación arriba mostrada; las geodésicas en tal caso son líneas rectas de modo tal que las partículas se mueven a lo largo de líneas rectas. En aquellas regiones en donde el espacio-tiempo no es plano, la ecuación de Einstein impone restricciones al tipo de curvatura posible. A primera vista, la ley de gravitación de Einstein no se parece en nada al esquema de Newton. Para poder ver una similitud, debemos ver a los componentes gμν del tensor métrico como potenciales que describen al campo gravitacional. Hay diez de ellos, en lugar de un solo potencial que distingue a la teoría Newtoniana, y estos diez potenciales no sólo describen al campo gravitacional sino al sistema de coordenadas empleado.
Una vez que tenemos el tensor covariante de Ricci Rμν, aplicándole a dicho tensor con la ayuda de un tensor métrico g contravariante una contracción sobre sus dos índices obtenemos un escalar R (un tensor de orden cero) conocido como el escalar de Ricci:
R = gμν·Rμν
el cual viene siendo a fin de cuentas el resultado de una doble contracción llevada a cabo sobre el tensor de Riemann:
R = gμν·Rμν = gμν· gαβ·Rαμβν
Con el tensor de Ricci en nuestras manos, nuestro primer intento en construír una nueva teoría física con los tensores R = (Rαβ) y T = (Tαβ) parecería estar solucionado. Con los dos tensores de orden dos la curvatura geométrica del espacio-tiempo puede ser igualada con la presencia de la masa-energía que produce dicha curvatura. Esto fue precisamente lo que hizo Einstein. Pero las primeras aplicaciones no sólo produjeron resultados poco satisfactorios, sino inclusive contradictorios. La teoría correcta para describir la nueva realidad física requería una modificación del tensor de Ricci. El nuevo tensor construído modificando el tensor de Ricci resultó ser precisamente el tensor de Einstein definido de la siguiente manera:
Resulta claro que el tensor de Einstein G es esencialmente un tensor mixto de orden dos, y la diferencia entre el tensor de Ricci R y el tensor de Einstein G se observa con mayor claridad viendo la representación matricial de los componentes del tensor de Einstein:
La única diferencia entre el tensor de Einstein y el tensor de Ricci estriba en la diagonal principal, a la cual se le resta a cada uno de sus componentes la mitad del escalar de Ricci. Esta parece una diferencia mínima. Y sin embargo, es justo lo que se requiere para que la ecuación tensorial de la Relatividad General pueda ser utilizada para analizar y predecir fenómenos físicos reales.
Puesto que el tensor de Ricci es un tensor simétrico, y puesto que el tensor de Einstein lo único que hace es modificar las entradas en la diagonal principal, el tensor de Einstein también es un tensor simétrico.
El tensor de Einstein G posee una propiedad importante: es un tensor libre de divergencia.
PROBLEMA: Demostrar que la divergencia del tensor de Einstein es cero en todos los puntos.
La solución de este problema requiere demostrar que:
Gri;r = 0
El procedimiento usual consiste en llevar a cabo una doble contracción sobre la segunda identidad de Bianchi por medio del tensor métrico. La segunda identidad de Bianchi es:
Rαβμν;λ + Rαβλμ;ν + Rαβνλ;μ = 0
gαμ·[Rαβμν;λ + Rαβλμ;ν + Rαβνλ;μ] = 0
Rμβμν;λ - Rμβμλ;ν + Rμβνλ;μ = 0
Los dos primeros términos se convierten en las derivadas covariantes de tensores de orden dos:
Rβν;λ - Rβλ;ν + Rμβνλ;μ = 0
Hasta aquí hemos utilizado la propiedad esencial del tensor métrico según la cual:
gαβ;λ = 0
y siendo el tensor métrico conjugado una función del tensor métrico entonces:
gαβ;λ = 0
En otras palabras, hemos utilizado la propiedad de que en la diferenciación covariante el tensor métrico y el tensor métrico conjugado pueden ser metidos y sacados fuera de la operación comportándose como si fuesen las constantes de la diferenciación ordinaria. Por otro lado, para meter convertir el signo positivo a signo negativo en el segundo término se ha utilizado la propiedad de hemisimetría (antisimetría) del tensor de Riemann:
gαμ·Rαβλμ;ν = - gαμ·Rαβμλ;ν
gαμ·Rαβλμ;ν = - Rβλ;ν
gαμ·Rαβλμ;ν = - Rβλ;ν
Llevamos a cabo ahora una segunda contracción:
gβν·[Rβν;λ - Rβλ;ν + Rμβνλ;μ] = 0
Esto se simplifica a:
R;λ - Rμλ;μ + (- Rμλ;μ ) = 0
R;λ - 2 Rμλ;μ = 0
R;λ - 2 Rμλ;μ = 0
Entonces, haciendo uso del hecho de que:
(δμλ R);μ = δμλ (R);μ = δμλ R;μ = R;λ
lo último lo podemos reescribir de la siguiente manera:
(2 Rμλ - δμλR);μ = 0
Pero lo que tenemos dentro del paréntesis, si lo dividimos entre 2, es precisamente el tensor de Einstein. Entonces, juntando los dos índices arriba con la ayuda del tensor métrico, obtenemos el resultado deseado:
Gαβ;β = 0
Este es un resultado fundamental, porque si la derivada covariante del tensor de Einstein, o sea su divergencia, es cero, entonces del otro lado de la ecuación primaria de la Relatividad General la divergencia del tensor energía-tensión T también debe ser cero. En pocas palabras, el que la divergencia del tensor de Einstein sea cero implica la conservación de la energía-momentum.
Como lo acabamos de hacer arriba, con la ayuda del tensor métrico podemos convertir liberalmente al tensor de Einstein en un tensor contravariante de segundo orden:
Gαβ = Rαβ - ½gαβR = Gβα
el cual como se ha señalado aquí es un tensor simétrico. Y del mismo modo, podemos convertir al tensor de Einstein en un tensor covariante de segundo orden:
Gαβ = Rαβ - ½gαβ R = Gβα
En general, en notación tensorial compacta:
G = R - ½ g R
Posiblemente algunos lectores se encuentren confundidos con el hecho de que en las definiciones tensoriales que usan notación de componentes los índices puedan aparecer indistintamente como super-índices (superscriptos) o como sub-índices (subscriptos). Se hace una pausa aquí al lector para recordarle en una ecuación tensorial de orden n existe una libertad absoluta en la forma en la cual los componentes del tensor son especificados. Por ejemplo, la ecuación tensorial fundamental de la Relatividad General:
G = 8πT
podemos expresarla en forma de componentes ya sea como:
Gαβ = 8πTαβ
con ambos índices arriba, o como:
Gαβ = 8πTαβ
con ambos índices abajo.