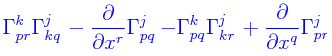El tensor de Riemann surge como consecuencia del análisis involucrado en dar respuesta a lo que parece ser una pregunta sencilla. Empezando con un tensor covariante V = (Vi) y tomando la derivada covariante del tensor primero con respecto a la coordenada x j y luego con respecto a la coordenada xk nos produce un tensor de tercer orden:
((Vi); j); k = (Vi); jk = Vi; jk
¿Pero que tal si tomamos primero tomando la derivada covariante del tensor primero con respecto a la coordenada xk y luego con respecto a la coordenada x j?:
((Vi); k); j = (Vi); kj = Vi; kj
¿Es importante el orden en el cual se lleve a cabo la diferenciación, o se puede decir que en general Vi; jk = Vi; kj?
En la diferenciación parcial ordinaria, no parece haber duda alguna al respecto, ya que las diferenciaciones múltiples se pueden llevar a cabo en el orden que sea:
Pero al estar trabajando con tensores, ya vimos que la diferenciación se tiene que llevar a cabo con nuevas reglas para que el objeto diferenciado pueda comportarse también como un tensor, se tiene que llevar a cabo usando la derivada covariante.
La respuesta a nuestra interrogante resulta ser una negativa rotunda, y tratándose de tensores el orden de la diferenciación sí es importante.
PROBLEMA: Demostrar que
Vp;qr - Vp;rq
no es igual a cero, y que por lo tanto el orden de la diferenciación covariante sí afecta el resultado final.
En el primer paso, evaluaremos primero la derivada covariante múltiple Vp;qr aplicando al pie de la letra la definición de la derivada covariante para un tensor covariante:
A continuación llevaremos a cabo la diferenciación covariante aplicando de nuevo al pie de la letra la definición de la derivada covariante para un tensor covariante:
El siguiente paso consiste en remover los paréntesis para tener lo siguiente:
Hemos obtenido ya Vp;qr. Repitiendo el procedimiento dado arriba, podemos obtener también Vp;rq, pero no es necesario hacerlo todo de nuevo, ya que basta con intercambiar el orden de los índices para obtener Vp;rq. Hecho esto, si restamos Vp;rq de Vp;qr obtenemos entonces:
Podemos renombrar los índices para poner en los cuatro términos al tensor Vj como producto:
Esto nos permite llevar a cabo la siguiente factorización:
A menos de que los símbolos de Christoffel sean todos iguales a cero, lo cual no ocurre en un espacio multi-dimensional plano, Vp;qr y Vp;rq no son iguales, son diferentes, y son diferentes precisamente en una cantidad como la mostrada en color azul entre los paréntesis. Dicha cantidad:
simbolizada tensorialmente como Rjpqr es precisamente lo que se conoce como el tensor de Riemann. El que Vp;qr ≠ Vp;rq tiene consecuencias geométricas profundas que serán analizadas posteriormente.
El tensor de curvatura de Riemann, o simplemente tensor de Riemann, es un tensor de orden cuatro, de modo tal que los componentes de dicho tensor no pueden ser visualizados con una representación matricial como ocurre con el caso de un tensor métrico g de orden 2. Estrictamente hablando, podemos definirlo como un tensor covariante de orden cuatro o bien -con la ayuda del tensor métrico g para subir el primer índice- como un tensor de orden (1,3), o sea un tensor covariante de orden 1 y contravariante de orden 3. En notación de índices, por lo tanto, es representado ya sea como Rabcd o como Rabcd. En el caso Rabcd (todos los cuatro índices abajo) llamamos al tensor un tensor de Riemann del primer género ó primera especie (first kind) mientras que en el caso Ra bcd (el primer índice elevado) llamamos al tensor un tensor de Riemann del segundo género ó segunda especie (second kind).
PROBLEMA: ¿Qué ventaja puede tener la representación del tensor de Riemann R como un tensor de primer género Rabcd sobre su representación como un tensor de segundo género Rabcd en notación de componentes?
Por la forma en que ha sido definido arriba el tensor de Riemann de segundo género como el “factor” que nos mide la no-conmutatividad de las diferenciaciones covariantes de segundo orden, debe resultar obvio que en un espacio 4-dimensional, por ejemplo, dicho tensor constará de 4x4x4x4 = 256 componentes, y si partimos “a la inversa” de cada una de las componentes Rabcd del tensor de primer género podemos obtener las 256 componentes que corresponden a la representación Rabcd del segundo género con la ayuda del tensor métrico conjugado g-1 = (gab) para subir el primer índice. El problema con esto es que al subir el primer índice inevitablemente habrá muchas componentes en las cuales el segundo, el tercero o el cuarto índice o varios de ellos puedan ser igual al primero, como la componente Rφtrφ, y esto se puede interpretar erróneamente como algo que invoca automáticamente la activación de la convención de sumación para índices repetidos. Al tensor de Riemann se le puede aplicar, desde luego, una operación de contracción tensorial mediante igualación de índices; esto es precisamente lo que se lleva a cabo con el tensor de Ricci, pero la definición original del tensor de Riemann de segundo género excluye la aplicación automática de la convención de sumación para índices repetidos. Esta es la razón del por qué varios autores contemporáneos hacen una mescolanza en la cual después de haber obtenido el tensor de Riemann de segundo género como lo hemos hecho arriba pasan casi de inmediato al uso del tensor de Riemann de primer género sin explicar claramente la razón que los orilló a ello (puesto que la operación de contracción tensorial se lleva a cabo entre un índice contravariante y un índice covariante, al estar todos los índices abajo en el tensor de Riemann de primer género no se aplica de ningún modo la convención de sumación y entonces no hay confusión alguna). Esta es una de las consecuencias de que el tensor de curvatura de Riemann o simplemente tensor de curvatura o simplemente tensor de Riemann, el cual es una generalización de la curvatura de Gauss K a dimensiones más altas, haya sido introducido en 1862 por Riemann y desarrollado en 1869 por Christoffel como una forma de describir completamente la curvatura en cualquier número de dimensiones mediante un “pequeño monstruo” mucho antes de que Einstein introdujera su convención de sumación para índices repetidos. Desafortunadamente tenemos una situación en la que por un lado los componentes del tensor de Riemann de segundo género Rabcd pueden ser obtenidos mediante una simple fórmula como podemos verlo en la expresión que tenemos arriba aunque bajo el riesgo de que en un momento de distracción se pueda interpretar accidentalmente la repetición del índice superior y alguno de los índices inferiores como una invocación automática a la convención de sumación, mientras que por otro lado para obtener los componentes del tensor de Riemann de primer género Rabcd en el cual no hay confusión se tienen que ir bajando con la ayuda del tensor métrico el índice en cada uno de ellos, lo cual nos duplica la cantidad de trabajo.
A menos de que se indique lo contrario, y esto tiene que ser estudiado y aclarado para cada caso en particular, en la evaluación de los componentes del tensor de Riemann de segundo género no se aplica automáticamente la convención de sumación para índices repetidos.
Formalmente, y en base al resultado obtenido al principio, el tensor de Riemann del segundo género se puede definir a partir de los símbolos de Christoffel (los cuales no son tensores) de la siguiente manera (¡obsérvese con detenimiento el uso de la derivada parcial ordinaria, indicado por la coma puesta antes del índice utilizado para la diferenciación!):
Ra bcd = Γabd,c - Γabc,d + Γaμc Γμbd - Γaμd Γμbc
Puesto de manera más explícita:
Ra bcd =__________________________
∂(Γabd)/∂xc - ∂(Γabc)/∂xd + Γabc,d + Γaμc Γμbd - Γaμd Γμbc
∂(Γabd)/∂xc - ∂(Γabc)/∂xd + Γabc,d + Γaμc Γμbd - Γaμd Γμbc
Si utilizamos el tensor de Riemann para el estudio de un espacio de cuatro dimensiones como ocurre en el caso del espacio-tiempo de la Teoría General de la Relatividad, cada uno de los cuatro sub-índices del tensor de Riemann puede representar una de cuatro variables diferentes, así que un tensor de Riemann está especificado por un total de 4x4x4x4 = 256 componentes, lo cual nos puede parecer intimidante. Sin embargo, debido a las simetrías que presenta este tensor, no todas las componentes son independientes, lo cual reduce el número de componentes que tienen que ser calculadas de 256 a 36. Una de tales simetrías en el intercambio del tercer y cuarto índice es la siguiente:
Ra bcd = - Ra bdc
Imponiendo además la condición adicional:
Ra bcd + Ra cdb + Ra dbc = 0
el número de componentes independientes puede ser reducido posteriormente a 21, y si se satisface una identidad adicional el número de componentes puede ser reducido a 20.
Poniendo las componentes del tensor de Riemann R = (Rαβμν) del primer género en función de las componentes de un tensor métrico g, podemos obtener la siguiente expresión (de nueva cuenta, las comas en los sub-índices indican derivadas parciales ordinarias):
Rαβμν = (gαν,βμ - gαμ,βν + gβμ,αν - gβν,αμ)/2
Del mismo modo, trabajando sobre esta última relación podemos obtener varias identidades que resultan ser de gran utilidad para la evaluación de todos los componentes Rαβμν para cierta métrica. La primera identidad nos dice que si intercambiamos los primeros dos índices (α y β) entonces obtendremos el mismo componente pero con el signo invertido, lo cual equivale a decir que Rαβμν es antisimétrico en el primer par de índices:
Rαβμν = - Rβαμν
La segunda identidad nos dice que si intercambiamos los últimos dos índices (μ y ν) entonces también obtendremos el mismo componente pero con el signo invertido, lo cual equivale a decir que Rαβμν es antisimétrico en el segundo par de índices:
Rαβμν = - Rαβνμ
La tercera identidad nos dice que si intercambiamos el primer par de índices (α y β) con el segundo par de índices (μ y ν) entonces obtendremos el mismo componente, lo cual equivale a decir que Rαβμν es simétrico en el intercambio de los dos pares de índices:
Rαβμν = Rμναβ
Y por último, la cuarta identidad, nos dice que:
Rαβμν + Rανβμ + +Rαμνβ = 0
Esta última identidad es conocida como la primera identidad de Bianchi.
PROBLEMA: A partir de la definición del tensor de Riemann de primer género, demostrar las identidades:
Rαβμν = - Rβαμν
Rαβμν = - Rαβνμ
Rαβμν = Rμναβ
Rαβμν + Rανβμ + +Rαμνβ = 0
Rαβμν = - Rαβνμ
Rαβμν = Rμναβ
Rαβμν + Rανβμ + +Rαμνβ = 0
1) A partir de la definición de los componentes Rαβμν en función de los componentes derivados del tensor métrico:
Rαβμν = (gαν,βμ - gαμ,βν + gβμ,αν - gβν,αμ)/2
intercambiamos los índices α y β obteniendo lo siguiente:
Rβαμν = (gβν,αμ - gβμ,αν + gαμ,βν - gαν,βμ)/2
y tras un simple reacomodo:
Rβαμν = (-gαν,βμ + gαμ,βν - gβμ,αν + gβν,αμ)/2
Rβαμν = - Rαβμν
Rβαμν = - Rαβμν
2) Procediendo como lo hicimos arriba, intercambiando los últimos dos índices μ y ν:
Rαβνμ= (gαμ,βν - gαν,βμ + gβν,αμ - gβμ,αν)/2
y reacomodando:
Rαβνμ = (-gαν,βμ + gαμ,βν - gβμ,αν + gβν,αμ)/2
Rαβνμ = - Rαβμν
Rαβνμ = - Rαβμν
3) Intercambiando el primer par de índices con respecto al segundo par de índices (lo cual debe ser interpretado como dos operaciones, la primera siendo el intercambio de los índices α y μ, y la segunda siendo el intercambio de los índices β y ν):
Rμναβ = (gμβ,να - gμα,νβ + gνα,μβ - gνβ,αμ)/2
Podemos efectuar un ligero reacomodo de índices, haciendo además uso del hecho de que las derivadas parciales ordinarias se pueden llevar a cabo en cualquier orden, esto es:
gαβ,νμ = gαβ,μν
obteniendo así lo siguiente:
Rμναβ = ( gμβ,αν - gμα,βν + gνα,βμ - gνβ,αμ)/2
Por otro lado, puesto que el tensor métrico es simétrico, tenemos que:
gαβ = gβα
con lo cual lo anterior se nos reduce a:
Rμναβ = (gβμ,αν - gαμ,βν + gαν,βμ - gβν,αμ)/2
y con otro ligero reacomodo:
Rμναβ = ( gαν,βμ - gαμ,βν + gβμ,αν - gβν,αμ)/2
Rαβμν = Rμναβ
Rαβμν = Rμναβ
4) Finalmente, escribiendo la suma de los tres términos involucrados en la primera identidad de Bianchi tras obtener los otros dos términos mediante un intercambio de índices, y simplificando con la ayuda de la simetría de los componentes del tensor métrico:
Rαβμν + Rανβμ + Rαμνβ =
(gαν,βμ - gαμ,βν + gβμ,αν - gβν,αμ)/2
(gαμ,νβ - gαβ,νμ + gνβ,αμ - gνμ,αβ)/2
(gαβ,μν - gαν,μβ + gμν,αβ - gμβ,αν)/2
(gαν,βμ - gαμ,βν + gβμ,αν - gβν,αμ)/2
(gαμ,νβ - gαβ,νμ + gνβ,αμ - gνμ,αβ)/2
(gαβ,μν - gαν,μβ + gμν,αβ - gμβ,αν)/2
obtenemos el resultado final deseado, la primera identidad de Bianchi:
Rαβμν + Rανβμ + Rαμνβ = 0
PROBLEMA: Trabajando sobre un espacio de cuatro dimensiones y con la ayuda de las identidades demostradas en el problema anterior, demuéstrese que estas identidades reducen el número de componentes independientes de Rαβμν de 4x4x4x4 = 256 componentes a 6x7/2 = 21 componentes.
Puesto que Rαβμν = - Rβαμν, si hacemos α = β entonces tenemos Rααμν = - Rααμν, lo cual sólo puede ser cierto si Rααμν es cero. Del mismo modo, puesto que Rαβμν = - Rαβνμ, si hacemos μ = ν entonces tenemos Rαβμμ = - Rαβμμ, lo cual sólo puede ser cierto si Rαβμμ es cero. Esto quiere decir que Rαβμν = 0 en todos los casos en los que los primeros dos índices o en los que los últimos dos índices sean iguales. Con esto en mente, iremos contando los componentes que pueden ser diferentes de cero de acuerdo a tres tipos de posibilidades:
Tipo A: Este es el caso en el cual el primer par de índices es igual al segundo par de índices siendo el primer índice en un par menor que el segundo índice en el mismo par, o sea todas las posibilidades de Rαβαβ siendo α menor que β. Aquí podemos listar las siguientes posibilidades para un espacio de cuatro dimensiones:
R1212 , R1313 , R1414 , R2323 , R2424 , R3434
Tenemos un total de seis componentes independientes, que de acuerdo a las leyes de la combinatórica es igual a nA = nC2 = n(n-1)/2 para un espacio de n dimensiones (la cantidad de combinaciones posibles de n objetos tomados dos a la vez), o sea
nA = 4(4-1)/2 = 4·3/2 = 6 componentes
para un espacio de 4 dimensiones.
Tipo B: Este es el caso en el cual el primer índice es igual al tercer índice siendo el segundo índice y el tercer índice diferentes, o sea todas las posibilidades de Rαβαγ siendo β menor que γ. Aquí podemos listar las siguientes posibilidades para un espacio de cuatro dimensiones:
R1213 , R1214 , R1314, R2123 , R2124 , R2324
R3132 , R3134 , R3234 , R4142 , R4143 , R4243
R3132 , R3134 , R3234 , R4142 , R4143 , R4243
Tenemos un total de doce componentes independientes, que de acuerdo a las leyes de la combinatórica es igual a nB = 3·nC3 = n(n-1)(n-2)/2 para un espacio de n dimensiones, o sea
nB = 4(4-1)(4-2)/2 = 4·3·2/2 = 12 componentes
para un espacio de 4 dimensiones.
Tipo C: Este es el caso en el cual todos los índices son diferentes, teniendo como posibilidades a Rαβγδ ó a Rαγβδ , siendo α menor que β, siendo β menor que γ, y siendo γ menor que δ. Aquí podemos listar las siguientes posibilidades para un espacio de cuatro dimensiones:
R1234 , R1324
Tenemos un total de dos componentes independientes, que de acuerdo a las leyes de la combinatórica es igual a
nC = 2·nC4 = n(n-1)(n-2)(n-3)/12
para un espacio de n dimensiones, o sea
nC = 4(4-1)(4-2)(4-3)/12 = 4·3·2·1/12 = 2 componentes
para un espacio de 4 dimensiones.
Sumando las contribuciones individuales de cada uno de los tres tipos de componentes, podemos obtener una fórmula general que nos dá la cantidad de componentes independientes del tensor de Riemann para un espacio de n dimensiones:
n = nA + nB + nC
n = n(n-1)/2 + n(n-1)(n-2)/2 + n(n-1)(n-2)(n-3)/12
n = 6n(n-1)/12 + 6n(n-1)(n-2)/2 + n(n-1)(n-2)(n-3)/12
n = [6n² - 6n + 6n3 - 18n² + 12n + n4 - 6n3 +11n² - 6n]/12
n = n² (n² - 1) /12
n = n(n-1)/2 + n(n-1)(n-2)/2 + n(n-1)(n-2)(n-3)/12
n = 6n(n-1)/12 + 6n(n-1)(n-2)/2 + n(n-1)(n-2)(n-3)/12
n = [6n² - 6n + 6n3 - 18n² + 12n + n4 - 6n3 +11n² - 6n]/12
n = n² (n² - 1) /12
Para un espacio de cuatro dimensiones, la fórmula general que acabamos de obtener nos dá:
n = 4² (4² - 1) /12 = 16 (16 -1) /12 = (16)(15)/12 = 20
PROBLEMA: Hacer un listado de los componentes independientes de Rαβαγ para un espacio de cinco dimensiones.
Utilizando la clasificación de tres tipos dada en el problema anterior, tenemos los siguientes componentes independientes del tensor de Riemann para un espacio de cinco dimensiones:
Tipo A: Rαβαβ siendo α menor que β:
R1212 , R1313 , R1414 , R2123 , R1515
R2323 , R2424 , R2525
R3434 , R3535
R2323 , R2424 , R2525
R3434 , R3535
Tipo B: Rαβαγ siendo β menor que γ:
R1213 , R1214 , R1215 , R1314 , R1315 , R1415
R2123 , R2124 , R2125 , R2324 , R2325 , R2425
R3132 , R3134 , R3135 , R3234 , R3235 , R3435
R4142 , R4143 , R4145 , R4243 , R4245 , R4345
R5152 , R5153 , R5154 , R5253 , R5254 , R5354
R2123 , R2124 , R2125 , R2324 , R2325 , R2425
R3132 , R3134 , R3135 , R3234 , R3235 , R3435
R4142 , R4143 , R4145 , R4243 , R4245 , R4345
R5152 , R5153 , R5154 , R5253 , R5254 , R5354
Tipo C: Rαβγδ , siendo α menor que β, siendo β menor que γ, y siendo γ menor que δ:
R1234 , R1235 , R1245 , R1345 , R2345
R1324 , R1325 , R1425 , R1435 , R2435
R1324 , R1325 , R1425 , R1435 , R2435
Hay diez componentes del tipo A y diez componentes del tipo C, los cuales sumados a treinta componentes del tipo B nos dá un total de 50 componentes, lo cual está de acuerdo con la fórmula general:
n² (n² - 1) /12 = 5² (5² -1) /12 = (25)(24)/12 = 50
PROBLEMA: ¿Cuántos componentes independientes de Rαβαγ puede haber para un espacio de tres dimensiones? ¿Cuáles son estos componentes?
Para un espacio de tres dimensiones, el número de componentes posibles es, de acuerdo a la fórmula general:
n² (n² - 1) /12 = 3² (3² -1) /12 = (9)(8)/12 = 6
Estos componentes son los siguientes:
R1212 , R1313 , R2323 , R1213 , R2123 , R3132