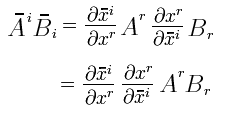En este caso, es fácil obtener las relaciones de transformación para convertir de coordenadas polares a Cartesianas (y viceversa):
X = r cos θ
Y = r sen θ
Y = r sen θ
Esto se puede extender hacia tres dimensiones, en donde necesitamos especificar una coordenada adicional. Es así como tenemos coordenadas Cartesianas (rectangulares) en tres dimensiones, coordenadas esféricas, coordenadas cilíndricas, y coordenadas afines.
Aquí resulta conveniente introducir coordenadas generalizadas (x0, x1, x2, x3 , ... , xn) con las cuales podemos simplificar nuestra notación, aplicándola en un espacio de tres dimensiones a las coordenadas cilíndricas:
(x0, x1, x2) = (r, θ, z)
y a las coordenadas esféricas:
(x0, x1, x2) = (r, θ, z)
A estas alturas, el lector cuyo interés principal es el estudio de la Teoría de la Relatividad se preguntará qué tiene que ver el estudio de las coordenadas cilíndricas y esféricas propias de un espacio tridimensional, con el espacio de cuatro dimensiones que utilizamos dentro de la Teoría de la Relatividad. No es difícil responder a esta pregunta, ya que podemos extender el alcance de las coordenadas cilíndricas y esféricas tal y como lo hicimos mediante coordenadas Cartesianas rectangulares hacia cuatro dimensiones con tan sólo agregar el cuarto componente, la coordenada del tiempo t (la cual supondremos que está multiplicada por la constante universal de la luz c a la cual le damos el valor de un metro por segundo, con el fin de darle a la cuarta coordenada la dimensión de longitud -en metros- en lugar de la dimensión de tiempo -en segundos- poniéndola así en igualdad total con las otras tres coordenadas que también miden longitud).
Así, las coordenadas cilíndricas en tres dimensiones son extendidas a:
(x0, x1, x2, x3) = (r,φ,z,t)
y las coordenadas esféricas en tres dimensiones son extendidas a:
(x0, x1, x2, x3) = (r,θ,φ,t)
Una vez familiarizados con las coordenadas generalizadas, podemos ver a continuación lo que tiene que ver con la aritmética de los tensores. Pero antes de entrar en materia, es importante dejar una cosa en claro. Al igual que en el caso de los vectores cuatri-dimensionales cuando los empezamos a manejar bajo el contexto de la Teoría Especial de la Relatividad, en donde se llevó a cabo la multiplicación de la coordenada del tiempo t por la velocidad de la luz c con el propósito de tener un vector [x, y, z, ct] en donde todos sus cuatro elementos estuviesen medidos en las mismas unidades de distancia (metros, kilómetros, millas, etc.), esto para no revolver peras con manzanas, del mismo modo en la aplicación de los tensores a los fenómenos físicos tampoco se acostumbra revolver peras con manzanas. Si uno de los componentes de un tensor está expresado en cierta dimensión física (presión, temperatura, humedad, tensión eléctrica, etc.) entonces todos los demás componentes del tensor estarán expresados en la misma dimensión física. Todos los componentes de un tensor están definidos en las mismas unidades. Esto es precisamente lo que nos permite llevar a cabo operaciones aritméticas con tensores, con la seguridad de que no estaremos sumando peras a manzanas.
PROBLEMA: Interpretar la siguiente relación utilizada con cierta frecuencia en las simplificaciones que se llevan a cabo al estar trabajando con coordenadas generalizadas:
usando como ejemplo ilustrativo en la interpretación el sistema de coordenadas polares (r,θ).
Para el caso en el cual a = b, la relación nos expresa lo obvio, que son las siguientes identidades matemáticas:
Y para el caso en el cual a ≠ b, la relación nos expresa la independencia de las coordenadas; ya que uno de los requisitos fundamentales de todo sistema de coordenadas es que la variación de cualquiera de sus componentes no produzca efecto alguno sobre las demás. Así, en las coordenadas polares el aumento o la disminución en la distancia radial es completamente independiente del cambio que se lleve a cabo en el ángulo que está siendo especificado, lo cual indicamos como:
Estos hechos los podemos resumir en la siguiente identidad matricial:
Pero también los podemos resumir utilizando la definición del tensor delta Kronecker como se ha hecho arriba en el planteamiento del problema. En la relación proporcionada se toman las derivadas parciales de los componentes que corresponden a un vector (tensor) covariante de orden uno. Sin embargo, la relación sigue siendo válida por las mismas razones cuando los componentes sobre los cuales se toman las derivadas parciales corresponden a un vector contravariante de orden uno:
Naturalmente, nos interesa saber cómo fue que llegó a nosotros la idea y la necesidad de tener que inventar y recurrir a algo como los tensores. Como ya se dijo, los tensores van directamente a la raíz de lo que es un cambio de coordenadas. Una de las relaciones matemáticas más importantes que involucran a funciones continuas de variables múltiples continuas es la definición del diferencial total. Para una expresión que depende de dos variables continuas como:
z = z (x, y)
el diferencial total de z se define como:
En un espacio de dos dimensiones, para un cambio de coordenadas Cartesianas (x,y) a coordenadas polares (r,θ), tendríamos dos expresiones:
En un espacio de tres dimensiones, para un cambio de coordenadas esféricas (r,θ,φ) a coordenadas rectangulares (Cartesianas) tendríamos tres expresiones:
En general, si se nos dá una función F suave y continua en n variables, definimos el diferencial total de dicha función F sobre cualquier número de dimensiones de la siguiente manera:
En notación de coordenadas generalizadas x1,x2, x3, ... , xn, el cambio incremental en la función continua suave F = F(x1,x2, x3, ... , xn) que resulta de los cambios incrementales dx1, dx2, dx3, ... , dxn en las variables x1,x2, x3, ... , xn estará dado por la siguiente relación(se recuerda aquí que los superíndices son simplemente índices, no exponentes):
Por definición, un tensor T cualesquiera de cualquier tipo y cualquier orden es un tensor cero O cuando todos los componentes del tensor son iguales a cero, lo cual implica que para cualquier tensor A diferente de cero:
A + O = A
Así, todos los 16 componentes de un tensor de orden 2 en un espacio cuatri-dimensional serán iguales a cero si ése tensor es un tensor cero. En el caso de tensores de orden dos (más no así en el caso de los tensores de orden 3 o mayor), los 16 componentes del tensor pueden ser representados en forma de matriz:
Del mismo modo, si el tensor mixto R ij klm = 0 para todos los valores de los índices i, j, k, l y m, entonces el tensor R de orden 5 será también un tensor cero, o sea R= O. (Obsérvese que un tensor de orden 5, en un espacio de dos dimensiones, está especificado por un total de 2x2x2x2x2 = 32 componentes.)
Los tensores, al igual que otros objetos matemáticos, también pueden ser sometidos a las operaciones usuales propias de la aritmética, y podemos hablar de una aritmética de tensores. Considérense dos tensores A y B que sean del mismo orden y del mismo tipo. Entonces podemos sumar dichos tensores, componente por componente, para obtener un tensor C:
C = A + B
La suma anterior está dada en notación tensorial. También podemos representarla de modo más explícito mostrando la suma de los componentes respectivos, por ejemplo:
Cij = Aij + Bij
Pij = Qij + Rij
Pij = Qij + Rij
Fijk mn = Hijk mn + Iijk mn
Obsérvese que no es notacionalmente correcto escribir A = Aij, ya que lo de la izquierda representa todos los componentes de un tensor mientras que lo de la derecha hace referencia a un solo componente, el componente con subíndices i y j. Sin embargo, podemos escribir A = (Aij), lo cual es notacionalmente correcto.
PROBLEMA: A partir de la definición de un tensor (covariante o contravariante) demuéstrese que la suma de dos tensores A y B del mismo orden y del mismo tipo producirá también un tensor C del mismo orden y del mismo tipo.
Considérense dos tensores covariantes de orden uno A y B. Por la definición de tensor, ambos obedecen la misma regla de transformación:
Sumando miembro a miembro ambas igualdades y simplificando:
Resulta evidente que sumando miembro a miembro los componentes respectivos de cada tensor, obtenemos un elemento C que también es un tensor ya que se transforma de acuerdo con la definición básica del tensor covariante, resultando también evidente que el tensor resultante es un tensor del mismo orden y del mismo tipo que los tensores de los cuales provino. De este problema resulta obvio también que la suma de dos tensores goza de la propiedad conmutativa, o sea:
A + B = C = B + A
y que el producto de un tensor por una constante multiplicativa resultará en un tensor.
Procediendo de modo similar al problema que acabamos de ver, podemos demostrar que el resultado es válido tanto para tensores contravariantes como para tensores covariantes, y que la resta o diferencia de dos tensores resultará tambié en un tensor del mismo orden y del mismo tipo (covariante o contravariante, según sea el caso).
Así como hay multiplicación de números, multiplicación algebraica y multiplicación de matrices, y del mismo modo en el que llevamos a cabo la multiplicación de dos cantidades P y Q:
P = p1 + p2
Q = q1 + q2
Q = q1 + q2
obteniendo:
PQ = (p1 + p2) (q1 + q2) = p1q1 + p1q2 + p2q1 + p2q2
podemos definir también el producto externo de dos tensores o simplemente el producto de dos tensores. Podemos demostrar formalmente, recurriendo a la definición del tensor, que el producto de dos tensores también tendrá las propiedades de un tensor.
PROBLEMA: Sean A = (Apqr) y B = (Bst) dos tensores. Demostrar que
Cpqsrt = Apq r·Bs t
es también un tensor.
Tenemos que demostrar que C = (Cpqsrt) es un tensor cuyos componentes son formados tomando los productos de los componentes de los tensores A y B. Si A y B son tensores, entonces deben obedecer las siguientes reglas de transformación:
Multiplicando ambas igualdades en sus lados respectivos:
Esto nos demuestra que el resultado final de la multiplicación de los dos tensores es un tensor de quinto orden, con índices contravariantes p, q y s e índices covariantes r, t, justificando la notación tensorial C = (Cpqsrt).
En general, la multiplicación de un tensor T1 de orden M por otro tensor T2 de orden N resultará en un tensor nuevo T de orden M+N formado por MxN componentes distintos. Así, el producto externo de dos tensores involucra simplemente la multiplicación ordinaria de los componentes del tensor, y es un tensor cuyo orden es simplemente la suma de los órdenes de los tensores que fueron multiplicados.
En ciertos textos se acostumbra denotar el producto externo de dos tensores S y T de la siguiente manera:
[ST]
En otros textos también se utiliza para denotar la misma operación del producto externo de dos tensores un círculo con una cruz puesta adentro:
S⊗T
Esta última notación tal vez le resultará familiar a los que son afectos al lenguaje de las matemáticas puras. Es ni más ni menos que la definición del producto Cartesiano utilizado para formar n-plas ordenadas de números. A manera de ejemplo de este concepto, si tomamos dos matrices distintas 2x2 y las multiplicamos no en el sentido usual de la multiplicación de matrices sino en el sentido del producto Cartesiano para así formar una nueva matriz a partir del producto de las matrices de base, tendremos algo como lo siguiente:
Inspirados en lo anterior, a continuación tenemos el resultado del producto tensorial externo de dos tensores U y V de orden dos en un espacio multi-dimensional indefinido cuyas componentes acomodadas en forma de matriz producen el siguiente resultado:
Debe resultar obvio que el producto externo de dos tensores de orden uno como:
T1 = (x1, x2, x3, x4)
T2 = (x1, x2, x3, x4)
T2 = (x1, x2, x3, x4)
nos resultará en un tensor de orden dos que contendrá todas las combinaciones posibles de productos xαxβ, de modo tal que en un espacio de cuatro dimensiones el tensor resultante estará compuesto por 16 componentes.
PROBLEMA: Dados los tensores:
A = (Aij)___B = (Bk)
obtener las componentes del producto externo de estos dos tensores en un espacio de dos dimensiones.
En un espacio de dos dimensiones, el tensor mixto A tendrá el siguiente conjunto de elementos:
{A11, A21, A12, A22}
mientras que el tensor covariante B tendrá el siguiente conjunto de elementos:
{B1, B2}
El producto externo de los tensores A y B, al cual simbolizaremos como C:
C = A⊗B
contendrá todas las combinaciones posibles de pares de productos de elementos del tensor A y de elementos del tensor B, o sea:
{A11B1, A21B1, A12B1, A22B1, A11B2, A21B2, A12B2, A22B2}
El tensor C termina siendo un tensor mixto de orden tres, cuyos componentes son Cijk = AijBk. Si los componentes del tensor A tienen unidades físicas de fuerza (newtons) y los componentes del tensor B tienen unidades físicas de distancia (metros) entonces los componentes del tensor C tendrán las unidades físicas que corresponden a la unidad compuesta, en este caso de energía (joules).
Un caso especial del producto de dos tensores ocurre cuando multiplicamos dos tensores del mismo orden e igualamos dos de sus índices, lo cual tiene una consecuencia directa e inmediata: la convención de sumación para índices repetidos entra automáticamente en acción. Pero antes de entrar en la definición de este producto muy especial de dos tensores, haremos un repaso de un concepto elemental que se aprende en los primeros cursos de matemáticas o de física intermedia: el producto de dos vectores, los cuales como ya se ha dicho en realidad son tensores de orden uno.
PROBLEMA: Redefinir, en lenguaje tensorial, el concepto vectorial del producto escalar (ó producto punto) de dos vectores, usando para ello dos vectores de un espacio cuatri-dimensional Cartesiano.
Empezamos con dos vectores A y B cuyas componentes respectivas son las siguientes:
A = (a1, a2, a3, a4)
B = (b1, b2, b3, b4)
B = (b1, b2, b3, b4)
Del análisis vectorial se sabe que el producto escalar de estos vectores está dado por:
A·B = a1b1 + a2b2 + a3b3 + a4b4
Redefinimos ahora ambos vectores como dos tensores A y B (siguen siendo lo mismo) de orden uno, definiendo a uno de ellos como un tensor covariante y al otro como un tensor contravariante, empleando notación de índices y coordenadas generalizadas:
A = (x1, x2, x3, x4)
B = (x1, x2, x3, x4)
B = (x1, x2, x3, x4)
El producto de los dos tensores A y B será entonces:
AB = (x1x1 + x2x2 + x3x3 + x4x4)
Un momento de reflexión nos revela que, gracias a la forma en la que hemos escrito lo anterior, podemos utilizar la convención de sumación:
AB = (xαxα)
Como resultado de esta operación de multiplicación de los tensores del mismo orden A y B, que definimos formalmente como contracción de tensores, vemos que partiendo de dos tensores de orden uno la operación de contracción abate el orden de cada uno de ellos convirtiéndolo en un tensor de orden cero, o sea en un escalar.La anterior definición puede ser generalizada a dos tensores de cualquier orden implementando el siguiente procedimiento:
Para llevar a cabo la contracción de dos tensores, igualamos uno de los índices superiores de un tensor con uno de los índices inferiores del otro tensor, sumando los productos de las componentes sobre los índices repetidos al entrar en acción automáticamente la convención de sumación. Esto tiene el efecto de disminuír el orden total de los dos tensores.
Para que la definición dada arriba sea válida, se requiere que los índices igualados correspondan a un índice covariante y a un índice contravariante.
Al llevar a cabo una contracción, los índices utilizados de la contracción desaparecen del tensor original. En la simbología del tensor resultante, simplemente se borran los índices que fueron contraídos.
La operación de contracción se puede aplicar inclusive a un mismo tensor siempre y cuando haya por lo menos dos índices que puedan ser igualados (con lo cual entra en acción de inmediato la convención de sumación), como lo demuestra el siguiente
PROBLEMA: Suponiendo que la contracción de un tensor nos produce otro tensor, ¿cuántos tensores diferentes pueden ser creados mediante la contracción repetida del tensor T = (Tijkl)?
El tensor que nos ha sido dado es un tensor de orden cuatro. La primera contracción la podemos llevar a cabo igualando el superíndice i con el superíndice k, haciendo i = k = u:
Tujul = T1j1l + T2j2l + T3j3l + T4j4l + ... + Tnjnl = Tjl
La segunda contracción la podemos llevar a cabo igualando el superíndice i con el superíndice l, haciendo i = l = u:
Tujku = T1jk1 + T2jk2 + T3jk3 + T4jk4 + ... + Tnjkn = Tjk
La tercera contracción la podemos llevar a cabo igualando el superíndice j con el superíndice k, haciendo j = k = u:
Tiuul = Ti11l + Ti22l + Ti33l + Ti44l + ... + Tinnl = Til
La cuarta contracción la podemos llevar a cabo igualando el superíndice j con el superíndice l, haciendo j = l = u:
Tiuku = Ti1k1 + Ti2k2 + Ti3k3 + Ti4k4 + ... + Tinkn = Tik
En todos los casos anteriores obtenemos tensores con dos índices libres, o sea tensores de orden dos. La operación de contracción entre dos índices abate el orden de 4 a 2, pudiendo obtenerse de este modo cuatro tensores diferentes a partir del tensor original.
La contracción repetida (doble contracción) aplicada sobre el tensor T = (Tijkl) nos produce en todos los casos los tensores (Tuvuv) y (Tuvvu). Y como en cada uno de estos dos tensores tenemos dos índices monigote iguales, lo cual requiere la aplicación por partida doble de la convención de sumación reduciéndolo todo a un simple número, a un escalar, podemos ver que para el tensor T del problema la doble contracción nos produce dos tensores de orden cero, o sea dos invariantes.
Se concluye en la resolución de este problema que se pueden generar hasta seis tensores diferentes a partir del tensor T = (Tijkl) mediante la operación de contracción.
PROBLEMA: Escribir los tensores que nos resultan de las siguientes contracciones:
1) T = (Tijkmlmnp)
2) T = (Tabcdeafgh)
3) T = (Tpqrsqstu)
4) T = (Tabijkmabkms)
1) En el tensor T = (Tijkmlmnp) de orden ocho tenemos el cuarto índice superior y el segundo índice inferior iguales (m), con lo cual la contracción automáticamente entra en efecto dejándonos el tensor de orden seis T = (Tijklnp).
2) En el tensor T = (Tabcdeafgh) de orden nueve tenemos el primer índice superior y el primer índice inferior iguales (a), con lo cual la contracción automáticamente entra en efecto dejándonos el tensor de orden siete T = (Tbcdefgh).
3) En el tensor T = (Tpqrsqstu) de orden ocho tenemos el primer índice superior y el primer índice inferior iguales (q) y además tenemos el último índice superior y el segundo índice inferior iguales, con lo cual la contracción automáticamente entra en efecto dejándonos el tensor de orden seis T = (Tprtu).
4) En el tensor T = (Tabijkmabkms) de orden once tenemos cuatro índices superiores que son iguales a cuatro índices inferiores (a,b,k,m), con lo cual al entrar en efecto la contracción nos deja un tensor de orden tres, el tensor T = (Tijs).
PROBLEMA: Usando directamente la definición de tensor, demuéstrese que el producto de un tensor contravariante A de orden uno por un tensor covariante B también de orden uno, ambos de la misma dimensión, nos producirá una invariante sin importar la dimensión (el número de coordenadas o componentes) involucrados.
Queremos demostrar que siendo A un tensor contravariante de orden uno y siendo B un tensor covariante también de orden uno se debe cumplir la siguiente relación:
A·B = A·B
Si A = (Ai) es un tensor contravariante de orden uno y B = (Bi) es un tensor covariante de orden uno, entonces de acuerdo a la definición básica del tensor tenemos lo siguiente (la convención de sumación está aplicada en ambos casos en virtud de los índices repetidos, y es la que nos fija la dimensión o el número de componentes de ambos tensores):
Multiplicando directamente ambas igualdades miembro a miembro:
Aquí podemos aplicar la regla de la cadena que para derivadas ordinarias es:
y que para derivadas parciales es:
con la cual:
Entonces:
Puesto que tenemos índices repetidos en ambos lados de la igualdad, al entrar en acción la convención de sumación los productos se reducen a un escalar, a un simple número, que es el mismo en ambos casos.
En notación tensorial compacta:
A·B = A·B
Esto significa que el producto de dos tensores, ambos de orden uno, el uno contravariante y el otro covariante, permanece igual después de haberse llevado a cabo un cambio de coordenadas. Puesto que un tensor de orden uno es en realidad un vector, lo que hemos hecho en la resolución de este problema ha sido formalizar matemáticamente y de manera rigurosa, a partir de la definición de tensor, el producto escalar de dos vectores. El hecho de haber utilizado tensores del mismo orden en la resolución de este problema hizo que, implícitamente, al entrar en acción la convención de sumación se llevara a cabo la contracción del producto de ambos tensores reduciéndose todo a un escalar.
Pero lo que acabamos de ver tiene repercusiones profundas por el hecho de que el producto interno de dos tensores no sólo es una invariante para dos tensores de orden uno. También resulta ser una invariante para el producto interno de dos tensores de orden dos.
PROBLEMA: Demostrar que la contracción del producto externo de dos tensores, siendo uno de ellos un tensor contravariante de orden dos y el otro un tensor covariante de orden dos, ambos de la misma dimensión, nos produce un escalar, y por lo tanto es una invariante.
Este problema es simplemente una repetición del procedimiento llevado a cabo en el problema anterior, excepto que ahora utilizamos tensores de orden dos en lugar de tensores de orden uno.
Si A = (Aij) es un tensor contravariante de orden dos y B = (Bij) es un tensor covariante también de orden dos, entonces de acuerdo a la definición básica del tensor tenemos lo siguiente (la convención de sumación está aplicada en ambos casos en virtud de los índices repetidos, y es la que nos fija la dimensión o el número de componentes de ambos tensores):
Multiplicando directamente ambas igualdades miembro a miembro:
Aplicando la regla de la cadena para derivadas parciales ordinarias tenemos entonces:
Nuevamente, puesto que tenemos índices repetidos en ambos lados de la igualdad, al entrar en acción la convención de sumación los productos se reducen a un escalar, a un simple número, que es el mismo en ambos casos, y tenemos nuevamente, en notación tensorial compacta:
A·B = A·B
Lo que acabamos de obtener no es un resultado sin trascendencia, porque el procedimiento que hemos aplicado en los últimos dos problemas, válido tanto para un par de tensores covariante y contravariante de orden uno como para un par de tensores covariante y contravariante de orden dos, es válido para cualquier par de tensores siempre y cuando en un espacio N-dimensional a cada índice covariante en un tensor corresponda un índice contravariante en el otro, y esto es válido incluso para tensores mixtos, de modo tal que si tenemos dos tensores mixtos A y B de orden cuatro tales que A = (Aijkl) y B = (Bijkl), entonces también se cumplirá la igualdad tensorial del producto de contracción de tensores A·B = A·B. Este resultado es de importancia fundamental porque todo lo que permanezca invariante va directamente al corazón de lo que trata la física: el principio de la conservación de la energía (invariancia de la energía), el principio de conservación de la cantidad de movimiento (invariancia del momentum), el principio de conservación del momento angular, en fin, todo lo que tenga que ver con cualquier fenómeno físico. En la teoría matemática de grupos aplicada a la Mecánica Cuántica, la prioridad es la búsqueda de las operaciones de simetría que dejan al sistema físico en sí intacto. Hemos encontrado por fin justo la herramienta matemática que necesitamos para poder llevar a la Teoría de la Relatividad del 4-espacio Lorentziano plano al 4-espacio curvo en donde a pesar de requerir una mayor cantidad de índices podremos anclar invariantes.
PROBLEMA: Demostrar que cualquier producto interno de dos tensores A = (Apr) y B = (Bqst) nos producirá un tensor de orden tres.
La demostración formal se debe llevar a cabo recurriendo a la definición del tensor. El producto interno se llevará a cabo aquí entre el índice p de A y el índice t de B igualando ambos índices, o sea haciendo p = t, lo cual activa la convención de sumación.
Si A = (Apr) es un tensor mixto, entonces por definición:
Y si B = (Bqst) es un tensor mixo, covariante de orden uno y contravariante de orden dos, entonces por definición:
Multiplicando ambos tensores haciendo j = n (que es la igualación de índices que corresponde a la igualación de índices p = t) para activar la convención de sumación sobre índices repetidos, tenemos:
Simplificamos ahora con la ayuda de la regla de la cadena:
Pero la igualación de índices p = t se traduce en ∂xt/∂xp = 1. Con esto llegamos a:
Esto nos demuestra que (AprBqsp) es un tensor de orden tres. Obsérvese que fue necesario cambiar el sub-índice en B de t a p en la última expresión. Si en el producto original (AprBqst) llevamos a cabo una contracción entre el índice r y el índice q, o entre el índice r y el índice s, podemos demostrar que cualquier contracción entre los dos tensores A y B nos producirá un tensor de orden tres.