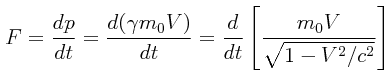Clásicamente, si una fuerza Fx actuando sobre un cuerpo de masa M le imprimía al cuerpo una aceleración ax de acuerdo con la fórmula Fx = Max dada por Newton, entonces para otro observador moviéndose a una velocidad constante V la fórmula seguirá siendo exactamente la misma en virtud de que las transformaciones de Galileo nos señalan que ax = a’x y por lo tanto F’x = Ma’x = Max, lo que a su vez implica F’x = Fx, y una misma fuerza permanece invariante (clásicamente) para otros observadores en movimiento relativo el uno con respecto al otro.
Sin embargo, de acuerdo con las transformaciones relativistas (las transformaciones de Lorentz) la aceleración de un cuerpo al pasar de un sistema de referencia S’ en movimiento a otro sistema de referencia S en reposo debe ser corregida de la siguiente manera:
O bien, multiplicando ambos miembros por la masa M:
Max = { 1 /γ3 (1 + Vux /c²)3 } Ma’x
Fx = { 1 /γ3 (1 + Vux /c²)3 } F’x
Fx = { 1 /γ3 (1 + Vux /c²)3 } F’x
De este modo, la fuerza F’x = Ma’x que es medida por el observador en movimiento ya no tiene el mismo valor que el que tiene cuando es medida por el observador en reposo, ya que tiene que ser corregida mediante el factor:
1 / { γ3 ( 1 + Vu’x /c²)3 }
con lo cual bajo las transformaciones de Lorentz la fuerza Newtoniana ha dejado de ser una invariante. Entonces debemos aceptar que una misma fuerza F cambie de valor al pasar de un marco de referencia a otro por el factor señalado, o bien debemos aceptar que la fórmula clásica F = Ma ha dejado de ser válida. Es razonable suponer que la fórmula F = Ma pierde su validez a altas velocidades porque esta fórmula implica que una fuerza constante puede acelerar a un cuerpo a velocidades ilimitadas si actúa por un tiempo largo. Por otro lado, si la velocidad de un cuerpo en un marco de referencia S’ es mayor que la velocidad de la luz, entonces no podemos llevar a cabo con las transformaciones de Lorentz la conversión del marco de referencia S’ a un marco de referencia en resposo S porque el factor γ se vuelve imaginario cuando la velocidad V del marco de referencia móvil es mayor que la velocidad de la luz c.
El concepto de una fuerza aplicada directamente sobre un cuerpo en movimiento es un concepto tan natural, tan esencial, tan básico, que antes que prescindir por completo de dicho concepto se vuelve deseable redefinirlo de alguna manera. Y para poder redefinirlo, tenemos que echar un vistazo a la forma en la cual Newton obtuvo la fórmula F = Ma.
Para poder desarrollar su esquema de dinámica clásica, Isaac Newton concibió un concepto sobre el cual descansa toda la estructura de su filosofía en lo que concierne a la dinámica. Para un cuerpo de masa m moviéndose a una velocidad v con respecto a un observador, si multiplicamos directamente la masa por la velocidad obtenemos una cantidad considerada como fundamental, una cantidad que Newton llamó la “cantidad de movimiento” de un cuerpo o momentum, frecuentemente simbolizada con la letra p (se ha utilizado notación vectorial para indicar que, por convención, el momentum de un cuerpo es una cantidad que posee la misma dirección y sentido en la cual se está moviendo el cuerpo con velocidad v):
p = mv
Así, para una masa de 5 kilogramos moviéndose a una velocidad de 4 metros por segundo, la cantidad de movimiento del cuerpo es:
p = (5 Kg)(4 m/seg)
p = 20 Kg-m/seg
p = 20 Kg-m/seg
A esta cantidad de movimiento se le asigna una dirección, la misma dirección que la que lleva el cuerpo al estar moviéndose. Puesto que la cantidad de movimiento p de un cuerpo es algo que tiene dirección y sentido, la fórmula es representada no en notación escalar sino en notación vectorial:
p = mv
Esta fórmula que nos fue dada por Newton no impone límite alguno a la velocidad a la cual se mueve el cuerpo, el cual se puede mover a una velocidad mayor que la velocidad de la luz, lo cual relativísticamente hablando es imposible.
Aunque no parezca obvio, entre las tres leyes del movimiento de Newton está injertado el concepto de que el momentum para una partícula o inclusive para todo un sistema de partículas es una cantidad que permanece invariable a menos de que intervenga una fuerza externa que lo modifique. Esta es esencialmente la ley de la inercia de Newton, pero ahora expresado como una de las leyes de conservación más básicas que pueda haber: el principio de la conservación de la cantidad de movimiento. Esta ley la podemos aplicar poniendo números a todo tipo de situaciones para obtener resultados concretos, como lo es el caso de un choque inelástico entre dos partículas:
En los anteriores diagramas: (a) antes de la colisión tenemos dos esferas moviéndose en la misma dirección, una de masa m1 moviéndose con velocidad u1 y otra de masa m2
moviéndose con velocidad u2, (b) la masa m1 moviéndose a una velocidad u1 que es mayor que la velocidad u2 eventualmente alcanza a la esfera que tiene por delante, ocurriendo un choque que supondremos que es perfectamente elástico y durante el cual a través de una fuerza de contacto F se lleva a cabo una transferencia de la cantidad de movimiento entre ambos cuerpos, (c) las masas se separan al impartirle la masa m1 algo de su momentum a la masa m2, adquiriendo cada uno de los cuerpos velocidades ν1 y ν2.
Si la cantidad de movimiento del sistema se conserva, entonces debemos tener como hecho dado para la anterior colisión que:
momentum antes del choque = momentum después del choque
PROBLEMA: Un observador que está en reposo con respecto a la Tierra observa una colisión en la cual una partícula de masa m1 = 3 kilogramos que se mueve a velocidad u1 = 4 metros/seg a lo largo del eje-x se aproxima a una partícula de masa m2 = 1 kilogramo que se mueve con velocidad u2 = -3 metros/seg también a lo largo del eje-x (obsérvese por el signo negativo que se está moviendo hacia la izquierda). Después de un choque frontal, el observador en Tierra encuentra que m1 lleva una velocidad de ν1 = 2 metros/seg mientras que m2 lleva una velocidad de ν2 = 3 metros/seg. Verificar que el momentum se ha conservado antes y después de la colisión.
momentum inicial = m1u1 + m2u2
momentum inicial = (3 Kg)(4 metros/seg) + (1 Kg)(-3 metros/seg)
momentum inicial = 9 Kg · m/seg
momentum inicial = (3 Kg)(4 metros/seg) + (1 Kg)(-3 metros/seg)
momentum inicial = 9 Kg · m/seg
momentum final = m1ν1 + m2ν2
momentum final = (3 Kg)(2 metros/seg) + (1 Kg)(3 metros/seg)
momentum final = 9 Kg · m/seg
momentum final = (3 Kg)(2 metros/seg) + (1 Kg)(3 metros/seg)
momentum final = 9 Kg · m/seg
Puesto que el momentum inicial es igual al momentum final, se concluye que la cantidad total de movimiento se conserva para este evento.
El principio de la conservación de la cantidad de movimiento es un principio que permanece válido al cambiar de un marco de referencia a otro usando las transformaciones clásicas de Galileo, como podemos comprobarlo con el siguiente problema que es un seguimiento al problema anterior:
PROBLEMA: Un segundo observador O’ que se mueve a una velocidad de 2 metros/seg relativa a la Tierra y a lo largo del eje-x observa el choque descrito en el problema anterior. ¿Cuáles serán los momentums antes y después del choque? ¿Se sigue conservando la cantidad de movimiento?
De acuerdo con las transformaciones clásicas de velocidad de Galileo:
u’1 = u1 - V = 4 metros/seg - 2 metros/seg = 2 metros/seg
u’2 = u2 - V = -3 metros/seg - 2 metros/seg = - 5 metros/seg
ν’1 = ν1 - V = 2 metros/seg - 2 metros/seg = 0
ν’2 = ν2 - V = 3 metros/seg - 2 metros/seg = 1 metro/seg
u’2 = u2 - V = -3 metros/seg - 2 metros/seg = - 5 metros/seg
ν’1 = ν1 - V = 2 metros/seg - 2 metros/seg = 0
ν’2 = ν2 - V = 3 metros/seg - 2 metros/seg = 1 metro/seg
Entonces:
momentum inicial = m1u’1 + m2u’2
momentum inicial = (3 Kg)(2 metros/seg) + (1 Kg)(-5 metros/seg)
momentum inicial = 1 Kg · m/seg
momentum final = m1ν’1 + m2ν’2
momentum final = (3 Kg)(0) + (1 Kg)(1 metro/seg)
momentum final = 1 Kg · m/seg
momentum inicial = (3 Kg)(2 metros/seg) + (1 Kg)(-5 metros/seg)
momentum inicial = 1 Kg · m/seg
momentum final = m1ν’1 + m2ν’2
momentum final = (3 Kg)(0) + (1 Kg)(1 metro/seg)
momentum final = 1 Kg · m/seg
Puesto que el momentum inicial es igual al momentum final, se concluye que la cantidad total de movimiento también se conserva para el segundo observador. Clásicamente, el principio de la conservación de la cantidad de movimiento sigue siendo válido al pasar de un sistema de referencia S a otro sistema de referencia S’.
Sin embargo, al utilizar las transformaciones de Lorentz en vez de usar las transformaciones clásicas de Galileo, descubrimos rápidamente que la cantidad de movimiento no se conserva invariable al pasar de un marco de referencia a otro. Esto lo podemos ver mejor considerando un experimento de balística en donde un observador O’ en un sistema de referencia S’ dispara un proyectil en la dirección del eje-y’. El proyectil penetra en un bloque que se encontraba inmóvil con respecto al observador O’:
La cantidad de masa m del proyectil que penetra en el bloque debe poder determinarse a partir de la componente en y’ del momentum del proyectil, el cual está dado por p’y = mu’y en donde m es la masa del proyectil medida por O’ que suponemos invariable.
Ahora considérese el mismo experimento desde el punto de vista del observador en reposo O para quien O’ se mueve a lo largo del eje x-x’ con velocidad V. Obviamente, antes de impactar con el bloque, la bala se estará moviendo no sólo hacia abajo sino también hacia la derecha con una cantidad de movimiento que podemos designar como p’x = mu’x, y después de haberse impactado con el bloque la combinación bala-bloque se seguirá moviendo hacia la derecha con una cantidad de movimiento que debe ser igual a p’x de acuerdo con el principio de la conservación de la cantidad de movimiento, además de moverse hacia abajo. Sin embargo, para el análisis simplificado que llevaremos a cabo, enfocaremos nuestra atención única y exclusivamente sobre lo que ocurre en el eje vertical.
Puesto que el orificio dejado por el proyectil forma un ángulo recto con la dirección del movimiento relativo, tanto O como O’ estarán de acuerdo en cuanto al valor de la distancia que el proyectil penetra en el bloque, y por lo tanto esperan que el valor de la componente en el eje-y del momentum del proyectil tenga el mismo valor para ambos de cumplirse el principio de conservación de la cantidad de movimiento. El momentum medido por O es py = muy en donde m es la masa del proyectil medida por O. De las transformaciones de Lorentz para la velocidad y teniendo en cuenta que u’x = 0, se obtiene:
uy = { u’y√ 1 - V²/c² } / { 1 + (V²/c²) u’x }
uy = u’y√ 1 - V²/c²
uy = u’y√ 1 - V²/c²
Entonces:
py = muy
py = mu’y√ 1 - V²/c²
py = mu’y√ 1 - V²/c²
Resulta indudable que p’y ≠ py, y por lo tanto el momentum clásico no se conserva bajo las transformaciones de Lorentz.
El concepto de la cantidad de movimiento es tan esencial y tan básico para la resolución de tantos problemas, que en vez de abandonarlo por completo optamos mejor por modificarlo adaptándolo a una nueva dinámica, la dinámica relativista. Esto fue precisamente lo que hizo Einstein. Lo más lógico es tomar la definición original que nos fue dada por Newton y modificarla de alguna manera agregándole algún factor de corrección relativista tal como el factor de corrección γ al cual ya estamos acostumbrados, obteniendo la definición de un momentum relativista. Si logramos obtener una definición correcta para el momentum relativista, entonces debemos obtener también un principio de conservación del momentum relativista que es a final de cuentas la razón de ser para haber definido desde un principio al momentum mu en la mecánica clásica como aquella cantidad que es conservada cuando no hay fuerzas exteriores actuando sobre un sistema (como lo es el caso de la colisión elástica entre dos cuerpos que acabamos de ver). Si nuestra definición de momentum relativista ha de ser válida, tiene que cumplir con los siguientes requisitos:
a) El momentum relativista es una cantidad que se debe conservar invariante para un sistema cerrado bajo las transformaciones de Lorentz.
b) El momentum relativista debe acercarse más y más a la definición clásica del momentum para velocidades bajas en comparación con la velocidad de la luz, o sea cuando V/c se va acercando a cero. Esto último nos lo impone la experiencia cotidiana que nos ha confirmado la validez del principio de la conservación de la cantidad de movimiento de un sistema a través de numerosos experimentos que se han llevado a cabo en donde los efectos relativistas son indetectables.
En la dinámica clásica, Newton formalizó el concepto de la fuerza interpretándola como la acción requerida para cambiarle a un cuerpo su cantidad de movimiento, dándole al tiempo absoluto un papel clave en esta interpretación. En el esquema de Newton, todo cuerpo mantiene su estado de reposo o un estado de movimiento rectilíneo constante (lo cual ocurre en el espacio exterior en donde no hay aire ni obstáculo alguno que le haga perder a un objeto la velocidad que lleva) mientras no intervenga una fuerza externa que modifique ese estado de reposo absoluto o de movimiento absoluto, y entre mayor sea la masa del cuerpo tanto mayor debe ser la fuerza requerida para hacerle cambiar su cantidad de movimiento. En este esquema, la fuerza tiene la siguiente definición matemática expresada usando infinitesimales:
La fuerza F es simplemente el cambio en la cantidad de movimiento p del cuerpo entre el lapso de tiempo requerido para provocar tal cambio en su cantidad de movimiento. En la notación vectorial utilizada para F, se le está dando a la fuerza la misma dirección que la dirección que toma el cambio de movimiento provocado sobre el cuerpo. Y puesto que p=mv, entonces:
F = d(mv)/dt
Si suponemos que la masa m del cuerpo es constante (lo cual no es cierto en todos los casos como el caso de un cohete que va lanzando combustible al exterior conforme se va despegando de su plataforma), entonces:
F = m * dv/dt
Pero el cambio en la velocidad con respecto al tiempo es simplemente la aceleración que experimenta el cuerpo al cambiar de velocidad. Entonces:
F = ma
Pero esta fórmula como está dada no puede ser sostenida dentro de la Teoría Especial de la Relatividad, porque implica que un cuerpo puede ser acelerado hasta alcanzar cualquier velocidad, incluso una velocidad superior a la velocidad de la luz, lo cual no es imposible. Obviamente, también aquí se requiere alguna modificación de conceptos. Pero ello empezará con la redefinición del momentum que sirve a su vez para definir el concepto de fuerza.
PROBLEMA: Hacer una gráfica que muestre el efecto relativista de la variación de la masa con la velocidad para un cuerpo con una masa de 1 kilogramo, graficando desde V = 0 hasta V = 0.9c.
Este es un problema de resolución directa que requiere evaluar algunos puntos que serán unidos por una curva de “mejor ajuste” en la gráfica. Para una velocidad de V = 0.7c, la masa relativista será:
m = m0/√ 1 - V²/c²
m = (1 Kg) / √ 1 - (0.7)² = 1.4 Kg
m = (1 Kg) / √ 1 - (0.7)² = 1.4 Kg
La gráfica resultante tiene el siguiente aspecto:
El aumento en la masa de un cuerpo de acuerdo con la velocidad del mismo frecuentemente provoca un efecto sorpresivo en quienes toman conocimiento por vez primera de este efecto, porque clásicamente la masa de un cuerpo era considerada como algo propio del cuerpo, inalterable, que nada tenía que ver con su velocidad; un kilogramo de tortillas de maíz seguía siendo un kilogramo de tortillas de maíz bajo cualquier ángulo que se le mirase. Sin embargo, en virtud de que la dinámica relativista impone un límite absoluto a la velocidad que puede alcanzar un cuerpo, la cual no puede ser mayor que la velocidad de la luz ya que en un caso así el término √ 1 - V²/c² se vuelve imaginario, si se trata de continuar aumentando la cantidad de movimiento de un cuerpo conforme se acerca a velocidades cada vez más cercanas a la velocidad al no poder rebasarse dicho límite entonces la cantidad de movimiento únicamente puede aumentar como resultado de un aumento en la masa. Es aquí en donde muchos acostumbrados a leer libros en los que sólo se dan unas cuantas fórmulas sin mayores explicaciones se preguntan: ¿De dónde sale esa masa? ¿Se está violando el principio de la conservación de la materia?
En realidad, la masa no está aumentando. El observador O’ que viaje en su marco de referencia S’ junto con el cuerpo verá a dicho cuerpo en reposo (con respecto a él) y no lo verá aumentar ni siquiera un miligramo. No hay creación alguna de materia salida de la nada. La materia “extra” es la que sería detectada por otro observador O en su marco de referencia S ante el cual el cuerpo se está moviendo a grandes velocidades. ¿Y de dónde sale ese incremento de masa para el observador O? En realidad, esa masa “extra” tiene que ver con el consumo de energía que hay que invertir para ir acercando al cuerpo a velocidades cada vez más cercanas a la velocidad de la luz. La aceleración de un cuerpo, el aumento en su cantidad de movimiento, es algo que no se logra gratuitamente, hay que invertir energía en el proceso. Para llevar a un cuerpo del reposo a una velocidad V = 0.7c se requiere el uso de cierta cantidad de energía que no saldrá de la nada. Esta energía va directamente al aumento en la cantidad de movimiento del cuerpo. Y si queremos subirle la velocidad a un cuerpo de V = 0.9998c a V = 0.99985c, ello requerirá también un consumo de energía. En realidad, esa masa “extra” aparente tiene que ver directamente con la energía que estamos invirtiendo en irle subiendo al cuerpo su velocidad. Esa energía no se va a la nada como tampoco puede sacar el cuerpo una cantidad de movimiento cada vez mayor sin que haya algo que lo continúe acelerando. Lo que estamos viendo en acción es ni más ni menos una equivalencia que llevó a Einstein a una de sus conclusiones más famosas, la cual encierra el secreto de la bomba atómica y la razón del por qué una estrella puede estar “ardiendo” liberando cantidades enormes de energía por millones de años sin “apagarse”. Esto es ya un asunto que nos lleva del tema del momentum relativista a la energía relativista de importancia tal que es necesario discutirlo por separado.
Teniendo en nuestras manos la definición del momentum relativista p = γmV, podemos proceder a reemplazar el concepto Newtoniano de la fuerza dinámica con el concepto relativista de fuerza, basándonos para ello en la definición original de fuerza como aquello que produce un cambio en la cantidad de movimiento de un cuerpo en cierto período de tiempo, en este caso del momentum relativista.
PROBLEMA: Una fuerza F actúa sobre un cuerpo en la misma dirección y sentido que su velocidad. Encontrar la expresión que corresponde a dicha fuerza acorde con la segunda ley de Newton.
La fuerza relativista es igual a la derivada del momentum relativista con respecto al tiempo:
Tomando la derivada:
Simplificando:
Finalmente, obtenemos la expresión que estábamos buscando:
De nueva cuenta, para velocidades suficientemente bajas en comparación a la velocidad de la luz, la expresión para la fuerza relativista se reduce a la expresión Newtoniana clásica F = ma.
Una aplicación práctica del concepto de la fuerza relativista está relacionada con el efecto que produce un campo magnético de intensidad B (el cual generalmente es representado con líneas de campo magnético que apuntan en la misma dirección de Norte a Sur en la cual apuntaría el imán de una brújula en puntos distintos de dicho campo) sobre una carga eléctrica que penetra en dicho campo a un ángulo recto al campo:
Una vez que la partícula con carga eléctrica ha penetrado a una velocidad V en una región en donde hay un campo magnético, la partícula experimenta una fuerza F determinada por la famosa “regla de la mano derecha” (usamos el dedo índice para indicar la dirección hacia la cual se está moviendo la partícula, usamos el dedo medio para apuntar la dirección de las líneas del campo magnético, obteniendo la dirección de la fuerza F con el dedo pulgar):
que actúa sobre la carga de modo tal que si el campo magnético es uniforme la pondrá en un movimiento de rotación inicialmente circular que sería perpetuo de no ser porque una particula cargada electricamente no puede permanecer por siempre girando en un campo magnetico dando vuelta tras vuelta ya que al estarse acelerando -vectorialmente hacia el centro de la rotación- la particula emite radiacion electromagnetica lo cual le va restando energía, con lo cual la partícula más que trazar un círculo va trazando una espiral hacia el centro:
Si imaginamos las líneas del campo magnético entrando hacia el monitor de la computadora como si fuesen unas flechas (con unas cruces indicando la cola en cada flecha), entonces podemos ver la acción de la rotación de la manera siguiente:
En este caso, la fuerza F no actúa en la misma dirección y sentido que la velocidad V del cuerpo, razón por la cual al llevar a cabo derivaciones de fórmulas relativistas de esta índole es necesario formalizar los cálculos con notación vectorial.
La magnitud de la fuerza F para una partícula con carga eléctrica atrapada en un campo magnético está dada por la siguiente relación:
║ F║ = F = qVB
Si esta fuerza está reteniendo a la carga con una fuerza centrípeta F = mV²/R de igual magnitud, entonces tenemos que la velocidad V estará dada por:
mV²/R = qvB
V = qBR/m
V = qBR/m
Esta relación es válida a velocidades suficientemente bajas en comparación con la velocidad de la luz. Pero para partículas energéticas con velocidades que se van aproximando a la velocidad de la luz, esta relación deja de ser válida, y tenemos que obtener la relación relativista para poder predecir correctamente lo que ocurre en una situación experimental.
PROBLEMA: Obtener la expresión para la velocidad relativista de una carga eléctrica que se mueve en un círculo de radio R y en ángulo recto con el campo magnético B.
En notación vectorial (usaremos negritas para representar cantidades vectoriales que tienen dirección y sentido), la segunda ley de Newton está definida como:
La fuerza relativista se obtiene utilizando en esta definición la masa relativista, con lo cual:
Pondremos ahora en el denominador la expresión V² como producto escalar V·V:
A continuación tomamos la derivada aplicando la regla de la cadena:
En el campo magnético, resulta claro que el vector velocidad V, siguiendo la dirección hacia la cual se está moviendo la carga, y el vector aceleración centrípeta dV/dt dirigido hacia el “centro” de la fuerza, son perpendiculares, y por lo tanto el producto punto de los mismos es cero:
Por otra parte, como vimos arriba, la fuerza que actúa sobre una carga a consecuencia de su interacción con el campo magnético es F = qvB, y además la magnitud de la aceleración centrípeta dirigida en la misma dirección que de la fuerza está dada por:
a = ║ dV/dt ║ = V²/R
Entonces:
A continuación se llevarán a cabo los pasos algebraicos necesarios para despejar para la velocidad V:
qB = m0V/R√ 1 - V²/c²
qB√ 1 - V²/c² = m0V/R
(qB)² (1 - V²/c²) = (m0V/R)²
(qB)² = [(m0/R)² + (qB/c)²] V²
V² = (qB)²/[(m0/R)² + (qB/c)²]
V² = (qBR)²/[(m0)² + (qBR/c)²]
V² = (qBR/m0)²/[1 + (qBR/m0c)²]
qB√ 1 - V²/c² = m0V/R
(qB)² (1 - V²/c²) = (m0V/R)²
(qB)² = [(m0/R)² + (qB/c)²] V²
V² = (qB)²/[(m0/R)² + (qB/c)²]
V² = (qBR)²/[(m0)² + (qBR/c)²]
V² = (qBR/m0)²/[1 + (qBR/m0c)²]
Finalmente, extrayendo raíz cuadrada, obtenemos el resultado deseado:
PROBLEMA: Supóngase que un haz de electrones describe un círculo de 0.2 metros de radio en un campo magnético uniforme con una densidad de flujo magnético igual a 0.03 teslas. ¿Cuál es la velocidad de dichos electrones?
Cada electrón en el haz de electrones posee la siguiente carga y masa en el sistema de unidades MKS:
q = 1.6 · 10-19 coulomb
m0 = 9.1 · 10-31 kilogramo
m0 = 9.1 · 10-31 kilogramo
Con esto:
qBR/m0 = (1.6 · 10-19 coulomb) (0.03 tesla) (0.2 metros)/9.1 · 10-31 kilogramo
qBR/m0 = 1.0549 · 109 metros/segundo
qBR/m0 = 3.5165 c
qBR/m0 = 1.0549 · 109 metros/segundo
qBR/m0 = 3.5165 c
Aplicando la fórmula obtenida en el problema anterior:
V = 3.5165 c / √ 1 + (3.5165)²
V = 0.962 c
V = 0.962 c
Trabajando sobre uno de los pasos intermedios en la derivación de la fórmula:
qB√ 1 - V²/c² = m0V/R
podemos obtener la siguiente relación:
qBR = m0V/√ 1 - V²/c²
qBR = γm0V
qBR = γm0V
Pero lo que tenemos en el lado derecho es simplemente el momentum relativista:
qBR = p
Esta también es otra relación útil en la resolución de problemas de este tipo.